-
ПОМОГИТЕ! ОЧЕНЬ ВАЖНО!
Сколько решений имеет уравнение, в зависимости от параматра а.
|x^2 -2|x|| + 1=a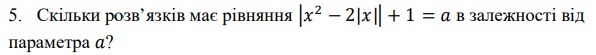
Ответы 5
-
a < 1 ⇒ нет решений * * * a ∈ ( - ∞ ; 1 ) ⇒ x ∈ ∅ * * *
-
Автор:
ezequielwqme - 6 лет назад
-
0
-
-
Да, об этом забыл)
-
Автор:
wendy - 6 лет назад
-
0
-
-
Спасибо за помощь)❤️
-
Автор:
sox71mp - 6 лет назад
-
0
-
-
1. Строим сначала график функции y = x² - 2x. Графиком квадратичной функции является парабола, ветви которого направлены вверх.
(1;-1) - координаты вершины параболы.
2.График функции y = x² - 2x симметрично отобразим относительно оси ординат, получим график функции y = x² - 2|x|
3. Нижнюю часть графика функции y = x² - 2|x| симметрично отобразим относительно оси Ох в положительную часть оси ординат, в результате получим график функции y = |x² - 2|x||
Графиком функции y = a-1 является прямая, параллельная оси Ох.
1) При a-1=0 откуда а=1 графики функций имеют три общих точек, следовательно, уравнение имеет три решения.
2) При 0 < a-1 < 1 откуда 1 < a < 2 графики пересекаются в 6 точках, следовательно уравнение имеет 6 решений.
3) При а - 1 = 1 откуда а=2 графики имеют четыре общих точек, следовательно, уравнение имеет ровно 4 решений
4) При a-1 > 1 откуда a>2 графики имеют две общих точек, значит уравнение имеет два решения

-
Автор:
duncanneal - 6 лет назад
-
0
-
-
|х²-2|х||+1=а|х²-2|х||=а-1если а=1 то есть 3 решениях²-2|х|=0[х²-2х=0;х=0;х=2[х²+2х=0;х=0;х=-2если а>1[х²-2|х|=а-1[х²-2|х|=-(а-1)1)х²-2х-(а-1)=0;х>0Д=4+4(а-1)>0 ;х=(2±√4а)/2=1±√ах1=1-√а<0х2=1+√2один решениех²+2х-(а-1)=0 ;х<0Д=4+4(а-1)=4а>0х=(-2±2√а)/2=-1±√ах=-1-√аодин решение2)х²+2|х|+(а-1)=0х²+2х+(а-1)=0Д=4-4(а-1)=8-4а>0;-4а>-8;а<21<а<2 ;2 решениях²+2х+(а-1)=02 решенияесли а€(1;2)то 6 решенияа≥2 2решенияесли а-1<0 ;а<1 то нет решения

-
Автор:
alonso7 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
выполните эти задания , ну или хотя бы парочку . Там где есть решение то с решением! Даю 15 баллов
-
Предмет:
Математика -
Автор:
estrellavbft - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Сколько решений имеет уравнение, в зависимости от параметра а. |x^2 -2|x|| + 1=a
-
что можно сказать в поздравлении ветерану с 1 сентября без стихов
-
Предмет:
Литература -
Автор:
aliza - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите написать сочинение на тему «Харизматичекая личность» про актера, певца и т.д. и почему я считаю его харизматичным человеком.
-
Предмет:
Русский язык -
Автор:
puppy7be7 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
