-
Изобразить на координаний плоскости множество точек (x; y), которые
удовлетворяют неравенство: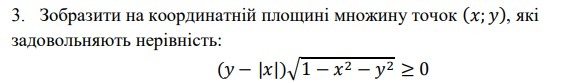
Ответы 1
-
Изобразить на координатной плоскости множество точек (x; y), которые удовлетворяют неравенству (y-|x|)√(1-x²-y²)≥0
Решение:
ОДЗ:
ОДЗ представляет собой множество точек, находящихся внутри окружности с центром (0; 0) и радиусом 1.
Так как √(1-x²-y²)≥0, то для выполнения неравенства требуется
Это "галочка" y=|x|. Решениями является все, что выше нее находится.
Изображение с координатной плоскостью прикреплено. Удовлетворяют неравенству те точки, которые лежат на пересечении синего и зеленого.

-
Автор:
georgenmhi - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Розв’яжіть нерівність 0,6x>0,4x+2
-
Отличия индустриального общества от информационного
-
Предмет:
Информатика -
Автор:
arturoulab - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как посчитать процент?
Допустим, мы должны ударить по мячу и попасть в ворота. При ударе, шанс попадания в ворота 20%. Какой шанс попасть по воротам (хоть 1 раз), если одновременно по воротам ударили 5 человек?
ответ будет 0.99968 ?-
Предмет:
Математика -
Автор:
louie5 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите с дз. На временна. 1.Ann was really tired yesterday. She (work) in the garden all day before i came. 2.My cousin (look) for his glasses for over an hour before he (find)them. 3.The lawyer (not come) to work yesterday.
4.What you ( do) the day before yesterday at 5?
5.Before she arrrived at the theatre he (already/buy) the tickets-
Предмет:
Английский язык -
Автор:
alfredjsde - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
