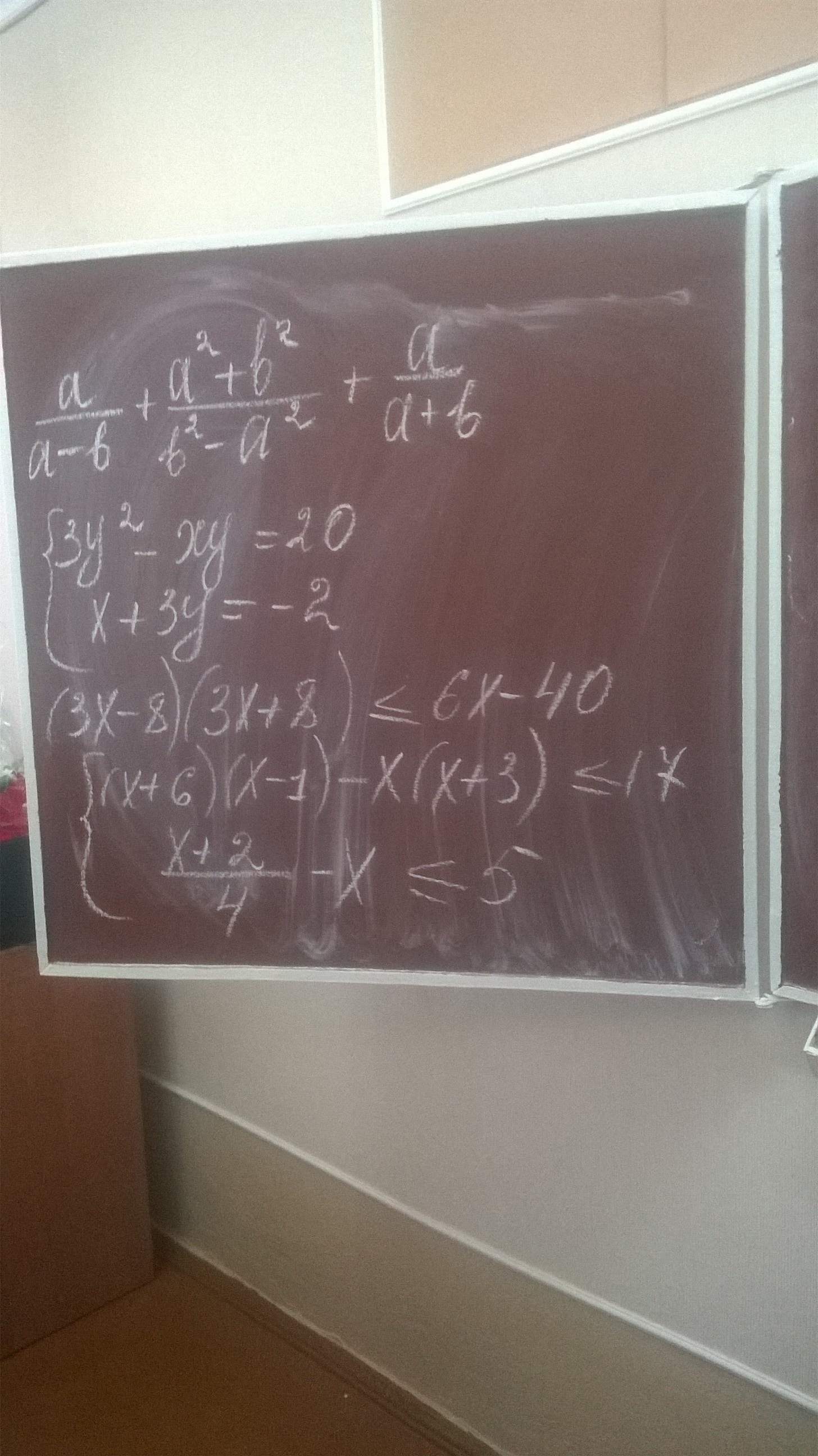Ответы 1
-
1) Вспомним формулу разности квадратов:
Приведём выражение к общему знаменателю:
2)
Парабола выглядит так (см. рисунок). Нам нужна область, где она меньше 0.
Ответ:
4)

-
Автор:
dominicksalazar - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Көп нүктенің орнына қажетті сөздерді қойып, тұрақты сөз тіркестерін жасаңдар.
Үлгі: тілінен ... тамған - тілінен бал тамған - сөзге шебер, шешен.
қысқа ... күрмеуге келмейді - кедейлік
қабағынан ... жауды - қатты ашуланды, кектенді
... жуытпау - қорғаштау
екі езуі екі ... жету - қуану
... түгі бар - батыр
Қажетті сөздер: жүрегінің, жіп, қар, шаң, құлағына.-
Предмет:
Қазақ тiлi -
Автор:
williams - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите решить пожалуйста
1.3(б)
1.4(а,б)-
Предмет:
Алгебра -
Автор:
craigabbott - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как обьяснить обещание устное и письменное ?
-
Предмет:
Русский язык -
Автор:
carleen - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Во сколько раз 4 меньше 12
-
Предмет:
Математика -
Автор:
rivera - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years