-
Помогите пожалуйста, и желательно с объяснением) пример на фотографии.
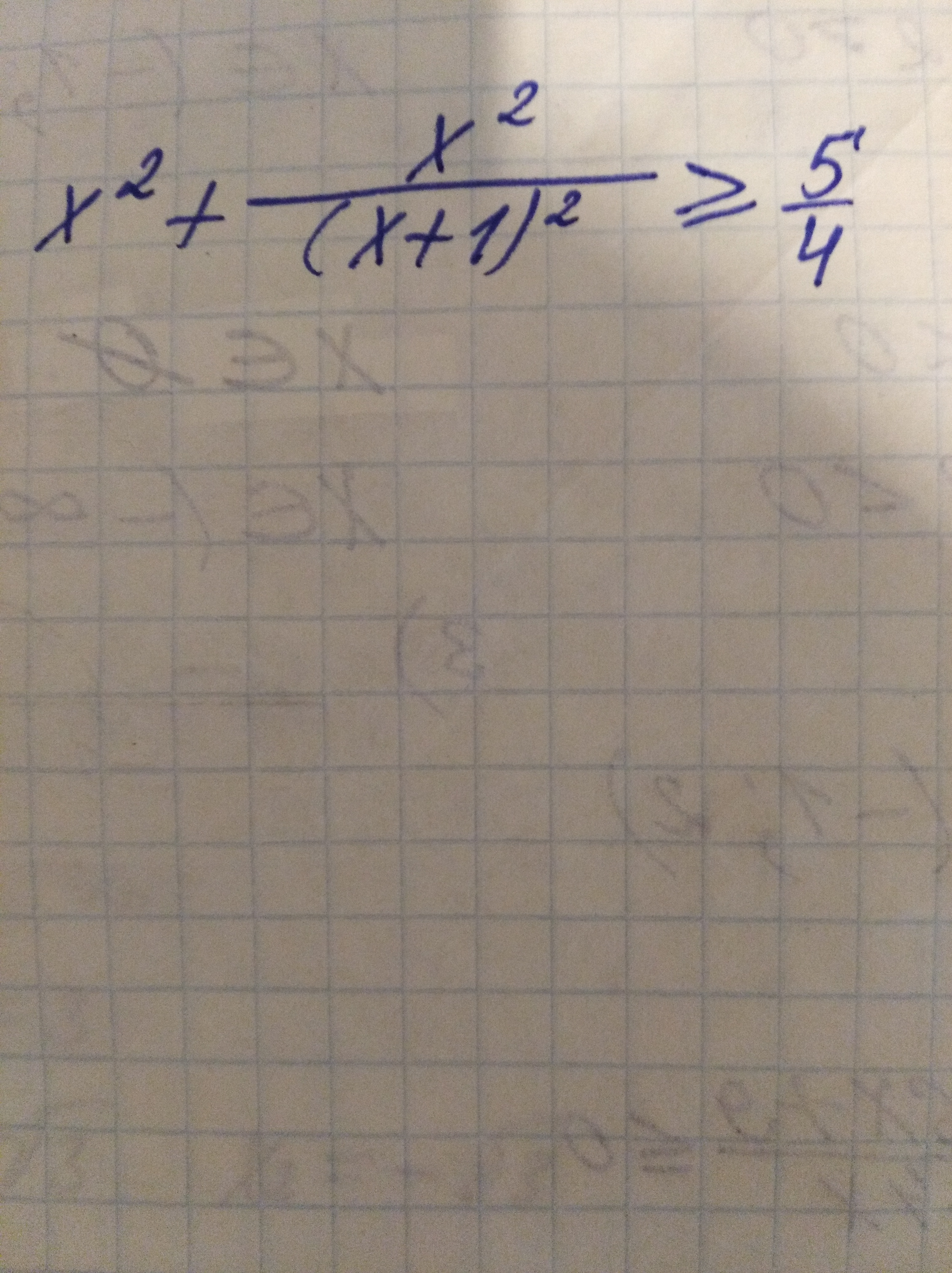
Ответы 1
-
task/29458435_7665 Решить неравенство x²+ x² / (x+1)² ≥ 5/4 .
решение: x² / (x+1)² +x² ≥ 5/4 ⇔ (x - x / (x+1) )² +2x²/(x+1) - 5/4 ≥0 ⇔
(x² / (x+1) )²+2* [x²/(x+1)]- 5/4 ≥0 Замена переменной: t = x²/(x+1)
t² + 2t - 5/4 ≥ 0 ⇔ ( t +5/2)(t - 1/2) ≥ 0 ⇒ t ∈ ( -∞ ; - 5/2 } ∪ [ 1/2 ; ∞) .
a) x²/ (x +1) ≤ - 5/2 ⇔2x²/ (x +1)+5/2 ≤ 0 ⇔(2x²+5x +5) /2(x+1) ≤ 0 ⇔
x+ 1 < 0⇒ x ∈ (- ∞ ; -1) .
! 2x²+5x +5 > 0 для всех x , т.к. a=2 >0 и D =5² -4*2*5 = -15 < 0
* * * 2x²+5x +5 = 2( x + 5/4)² + 15 /8 > 0 * * *
б) x²/ (x +1) ≥ 1 /2 ⇔ x²/ (x +1) -1 /2 ≥ 0 ⇔ (2x² - x - 1 ) / 2(x+1) ≥ 0 ⇔
(x + 1 /2) (x - 1) / (x+1) ≥ 0 || методом интервалов ||
" -" " +" " -" " +"
------------- (-1 ) ////////// [ - 1 / 2 ] -------------- [ 1 ] ///////////
x ∈ (-1 ; - 1 / 2 ] ∪ [ 1 ; ∞) .
объединяя решения пунктов a) и б) окончательно получаем
ответ : x ∈ ( - ∞ ; - 1) ∪ (- 1 ; 1/2 ] ∪ [ 1 ; + ∞) .
-
Автор:
froggertmhh - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Вітер плаче, вітер віє, дощ осінній дрібно сіє.
Тече туман у берегах ріки : течуть в тумані птиці над рікою
Будь ласка зробіть синтаксичний розбір цих двух речень.
-
Предмет:
Українська мова -
Автор:
caesar86 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
(1/4+2/3)•6/11
———————
(3/4-1/3):5/9-
Предмет:
Математика -
Автор:
checkerswillis - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Твір на тему що для мене значить мережа інтернет?
-
Предмет:
Українська мова -
Автор:
devinuqag - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите сделать морфемный разбор срочно прошу двух слов до боли и клочок текст с верху
-
Предмет:
Русский язык -
Автор:
shelby98 - 6 лет назад
-
Ответов:
6 -
Смотреть
-
