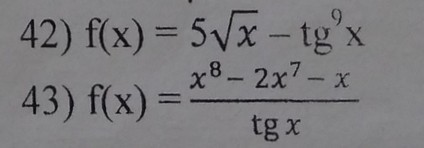Ответы 2
-
Соответственно, tan(x)=tg(x). Просто другое его обозначение.
-
Автор:
duchess - 6 лет назад
-
0
-
-
Вспомним правила дифференцирования частного двух функций и производную тангенса
Тогда:
Перейдем к примерам
Приведем последний пример к более благородному виду
Ответ.
;
-
Автор:
gideond2vx - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Понаблюдайте у каких растений происходит измение окраски листьев , какова она у разных растений
-
Предмет:
Биология -
Автор:
charlesriley - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите Пож И чтоб по действеям и чтобы было понятно Пож
-
Предмет:
Математика -
Автор:
ariasyuyl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ПОМОГИТЕ ПОЖАЛУЙСТА 50 БАЛЛОВ!!
Перепишите словосочетания, раскрывая скобки. Определите виды подчинительной связи в словосочетаниях с предлогами.
Поступать согласно (обстановка), вопреки (наше ожидание),грущу по (ты), скучаю по (вы),прибыл согласно (расписание), Обезвредили благодаря (оперативность), победили вопреки (обстоятельства),выполнили согласно (приказ), успели благодаря (собранность), добиться наперекор (судьба) , звучал подобно (гром) ,скучаю по (каникулы),горюю по (потеря) ,тоскую по (вы)-
Предмет:
Русский язык -
Автор:
augiemitchell - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Каким должен быть человек, чтобы про него в народе складывали песни?
Якою має бути людина, щоб про неї в народі складали пісні?
(Не большой ответ на вопрос, буду благодарен)-
Предмет:
Литература -
Автор:
maddie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years