Задать вопрос Регистрация
Помочь другим

  • N6. F(x) =x^-2 M(1;-1) F(x) =x^-3 M(-1;0) найти первообразную.

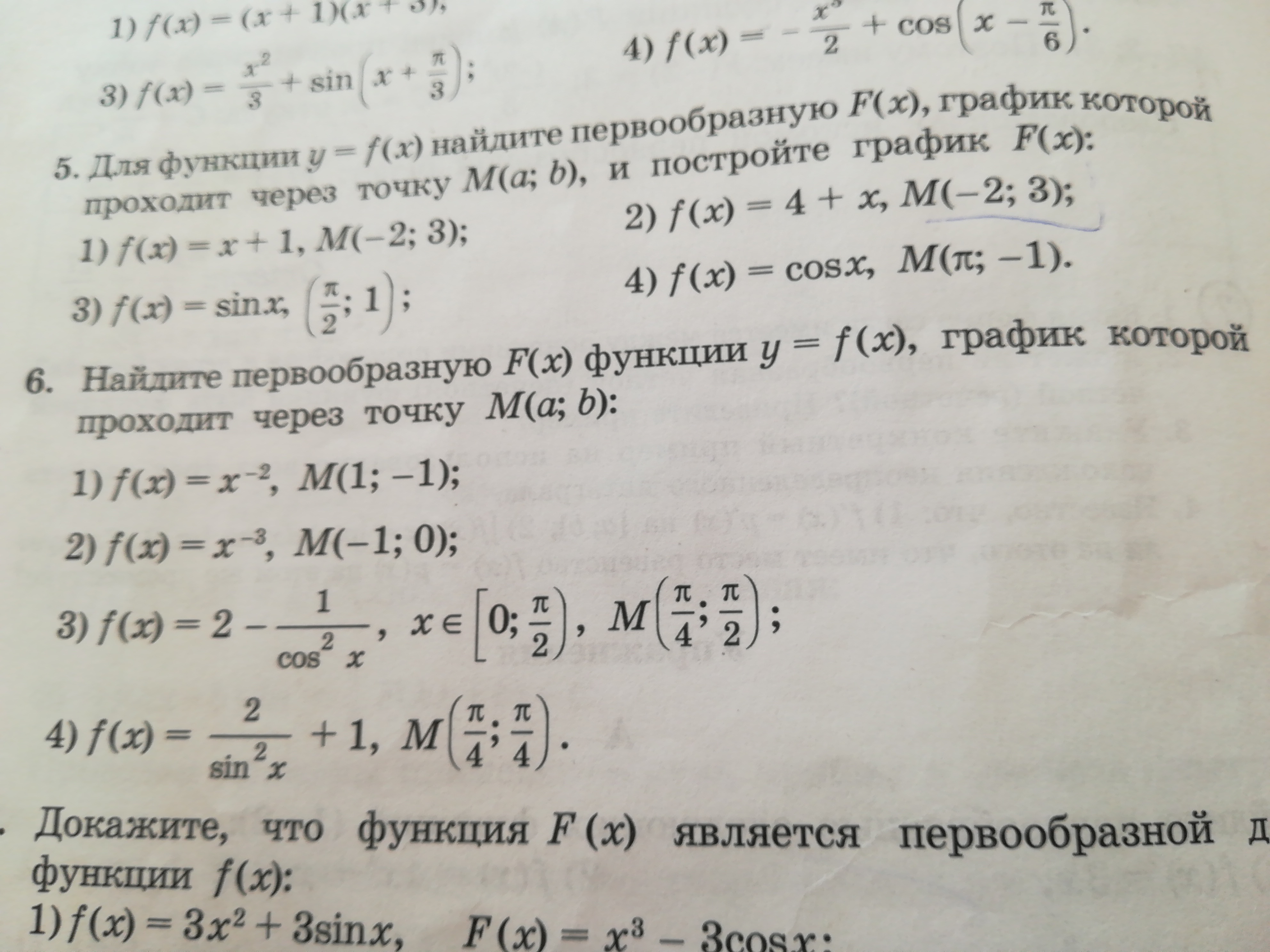
    question img

Ответы 1

  • Используя таблицу и правила нахождения первообразных, получим:

    f(x)=(-2+1)\cdot x^{-2+1}+C=-\dfrac{1}{x}+C

    Подставим координаты точки М в общий вид первообразной

    -1=-\dfrac{1}{1}+C\\ C=0

    Имеем первообразную \boxed{f(x)=-\dfrac{1}{x}}

    2) Аналогично с делаем и со следующим примером, т.е.

    f(x)=(-3+1)\cdot x^{-3+1}+C=-\dfrac{2}{x^2}+C

    И подставим координаты точки М, получим

    0=-\dfrac{2}{(-1)^2}+C\\ C=2

    Искомая первообразная \boxed{f(x)=-\dfrac{2}{x^2}+2}

    • Автор:

      allisson
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years