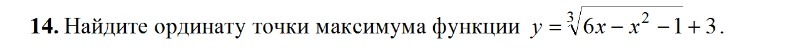Ответы 2
-
Находим производную, затем стационарную точку, затем ординату. Классика.
Доказывать, что эта стационарная точка и есть точка максимума не обязательно, ведь других точек нет, так что в связи с условием задания это очевидно.
Ответ: 5-
Автор:
baby doll4exp - 6 лет назад
-
0
-
-
Решение на фотографии

-
Автор:
hoover - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Задумали число увеличили его в 3 раза полученный результат увеличили еще в 4 раза Во сколько раз увеличилось число в итоге
-
Предмет:
Математика -
Автор:
lil mama - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Выбери из текста слова признаки которые помогут представить образ персонажей алдар-косе персонаж казахских сказок сын бедняка находчивые хитро алдар-косе защищает бедных обманывает и наказывает жадных богачей лентяев Глубцов
-
Предмет:
Русский язык -
Автор:
barleyreed - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- что такое научный метод?
-
граматика -це.... допоможіть будь ласка
-
Предмет:
Українська мова -
Автор:
lawrence - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years