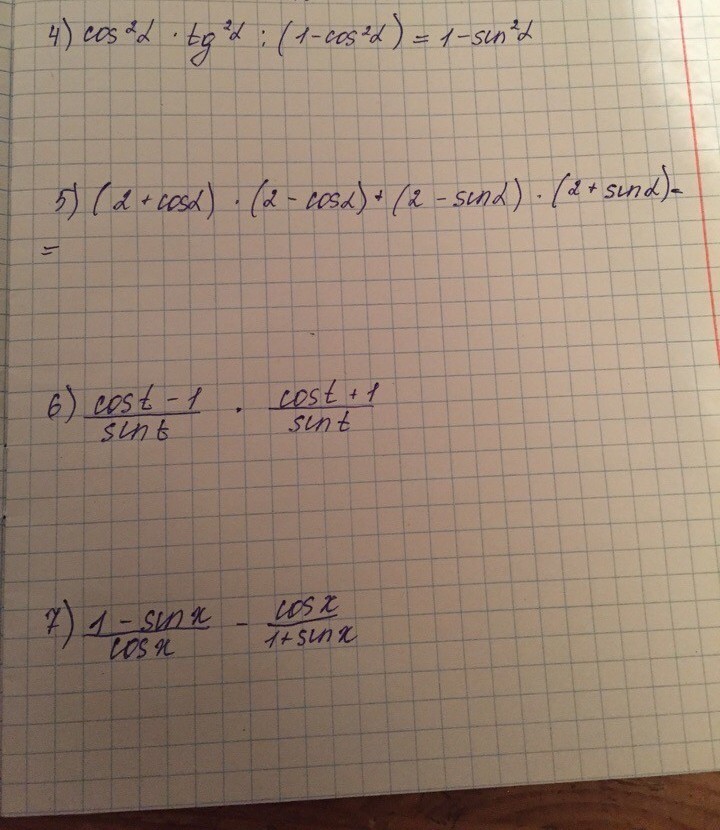Ответы 8
-
понял
-
Автор:
russell - 6 лет назад
-
0
-
-
Перезагрузите. Выйдите и снова зайдите .
-
Автор:
noeleq8h - 6 лет назад
-
0
-
-
смысле не верно
-
Автор:
brody - 6 лет назад
-
0
-
-
а в 4 1 или cos^2a
-
Автор:
aresio - 6 лет назад
-
0
-
-
Левая часть равенства равна 1 . Там нужно было упростить или доказать тождество?
-
Автор:
siennaaok7 - 6 лет назад
-
0
-
-
Вы правильно написали четвёртое задание?
-
Автор:
heaven - 6 лет назад
-
0
-
-
-
Автор:
syllableq9dq - 6 лет назад
-
0
-
-
4) cos²a*tg²a:sin²a = 1 - sin²a
ctg²a* tg²a= 1 - sin²a
1= cos²a - не верно
5) 4 - cos²a +4 - sin²a =8 -1=7
6) (cos²t - 1)/ sin²t= - sin²t / sin²t= -1
7) 1 - sin²x - cos²x/cosx*(1-sinx)=0
-
Автор:
edgar79 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
нужна сказка и маленьком жирафики и его маме
-
Предмет:
Литература -
Автор:
roysolis - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
провідник завдовжки 40 см по якому тече струм силою 1.5 А. розташований перепендикулярно до силових ліній однорідного магнітного поля , індукції якого дорівнює 0,2 Тл. Визначити модуль та напрям сили Ампера , що діє на провідник. Будь ласка дуже дуже треба
-
Предмет:
Физика -
Автор:
everettbluu - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Добрый вечер всем! Есть любители математики? Помогите, пожалуйста, решить.
-
Прошу, сделайте предложения с выделенными словами на английском и переведите их на русский язык , желательно чтобы предложения были оригинальны и составлялись без помощи гид-переводчика.
Спасибо за понимание .-
Предмет:
Английский язык -
Автор:
josue - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years