Задать вопрос Регистрация
Помочь другим

  • helpppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppppp

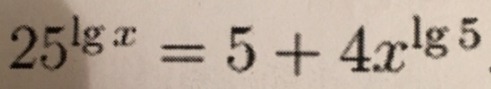
    question img

Ответы 2

  • I hope this helps you

    answer img

    • Автор:

      love81
    • 6 лет назад
    • 0
  • {25}^{lgx} = 5 + 4 {x}^{lg5} \\ {x}^{lg5} = {x}^{ \frac{ log_{x}5}{ log_{x}10} } = \\ = ({x}^{ log_{x}5 } ) ^{ \frac{1}{ log_{x}10 } } = {5}^{lgx} поэтому {25}^{lgx} = 5 + 4 {x}^{lg5} \\ ({5}^{lgx})^{2} - 4 \cdot {5}^{lgx} - 5 = 0 \\ y = {5}^{lgx} > 0\\ {y}^{2} - 4y - 5 = 0 \\ (y - 5)(y + 1) = 0 \\ y_1 = 5 \\ y_2 = - 1 < 0\\ y_2нам не подходит, т.к. y>0Возвращаемся к замене{5}^{lgx} = 5 \\ lgx = 1 \\ x = 10нам подходит, так как удовлетворяетОДЗ x>0Ответ :x=10
    answer img

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years