-
Даю 100 балов. Ребята помогите пожалуйста прошу. Теорема Безе:Докажите что многочлен F(x)делиться нацело на многочлен P(x) Если:
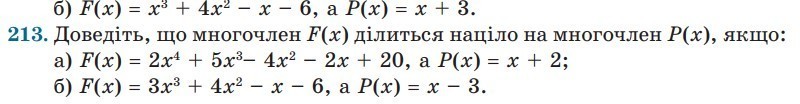
-
Предмет:
Алгебра -
Автор:
trufflesyigg - 6 лет назад
-
Ответы 3
-
Перезагрузите, там ещё решение верхнего.
-
Автор:
michaela75r9 - 6 лет назад
-
0
-
-
спасибо вам большое за решение
-
Автор:
kibblescollier - 6 лет назад
-
0
-
-
a)
F(x)=2x⁴+5x³-4x²-2x+20
P(x)=x+2
x+2=x - (- 2) => a= - 2
По теореме Безе остаток от деления F(x) на P(x) равен F{- 2).
F(-2) = 2·(-2)⁴+5·(-2)³-4·(-2)²-2·(-2)+20 =
= 2·16 - 5·8 - 4·4 + 2·2 + 20 =
= 32 - 40 - 16 + 4 + 20 = 0
Если F(-2) = 0, то это означает, что остаток равен нулю, следовательно, многочлен F(x)=2x⁴+5x³-4x²-2x+20 делится на P(x) = x+2 без остатка.
Ответ: многочлен F(x)=2x⁴+5x³-4x²-2x+20 делится на P(x) = x+2 без остатка.
б)
F(x)=3x³ + 4x²- x - 6
P(x)=x - 3
x - 3 => x=3
F(3) = 3·3³ + 4·3²- 3 - 6 = 81 + 36 - 3 - 6 = 108
Oстаток F(3) ≠0, следовательно, многочлен F(x)=3x³ + 4x²- x - 6 делится на P(x) = x-3 c остатком.
Ответ: многочлен F(x)=3x³ + 4x²- x - 6 делится на P(x) = x-3 c остатком, равным 108.
б) верхний
F(x) = x³ + 4x²- x - 6
P(x)=x + 3
x - (-3) => x= - 3
F(- 3) = (-3)³ + 4·(-3)²- (-3) - 6 = - 27 + 36 + 3 - 6 = 6
Oстаток F(3) ≠0, следовательно, многочлен F(x)=x³ + 4x²- x - 6 делится на P(x) = x+3 c остатком.
Ответ: многочлен F(x) = x³ + 4x²- x - 6 делится на P(x) = x+3 c остатком, равным 6.
-
Автор:
prestonnebk - 6 лет назад
-
0
-
-
Добавить свой ответ
- Можно пожалуйста 10 способов получения иодида калия - молекулярные уравнения. Очень срочно нужно!
-
Помогите ответить на вопрос!
II. Complete the following sentences with 3 to 5 words:
24. During the English Civil War Roundheads were the people mostly the merchants and traders who _______________________.
-
Предмет:
Английский язык -
Автор:
silviagoodman - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста . Не разбираюсь в временах это Past или Present simple ? Срочно !
-
Предмет:
Английский язык -
Автор:
micahmurray - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
4 примера сложносочинённые предложения
-
Предмет:
Русский язык -
Автор:
ziggyl8nv - 6 лет назад
-
Ответов:
2 -
Смотреть
-
