Задать вопрос Регистрация
Помочь другим

  • Выполните действия над комплексными числами и результат запишите в экспоненциальной форме.

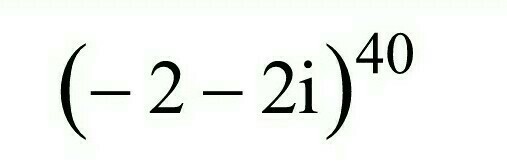
    question img

Ответы 1

  • Рассмотрим комплексное число:

    z=-2-2i

    Найдем его модуль и аргумент:

    |z|=\sqrt{(-2)^2+(-2)^2}=\sqrt{8}=2\sqrt{2}

    \arg z=\mathrm{arctg}\dfrac{-2}{-2}-\pi=\mathrm{arctg}1-\pi=\dfrac{\pi }{4}-\pi=-\dfrac{3\pi }{4}

    Запишем число в тригонометрической форме:

    z=2\sqrt{2} \left(\cos\left(-\dfrac{3\pi }{4}ight)+i\sin\left(-\dfrac{3\pi }{4}ight)ight)

    Для возведения в степень воспользуемся формулой Муавра:

    (ho\left(\cos\phi+i\sin\phiight))^n=ho^n\left(\cos n\phi+i\sin n\phiight)

    z^{40}=(2\sqrt{2})^{40} \left(\cos\left(-\dfrac{3\pi }{4}\cdot40ight)+i\sin\left(-\dfrac{3\pi}{4}\cdot40ight)ight)=\\=2^{40}\cdot(\sqrt{2})^{40} \left(\cos\left(-3\pi\cdot10ight)+i\sin\left(-3\pi\cdot10ight)ight=\\=2^{40}\cdot2^{20} \left(\cos\left(-30\piight)+i\sin\left(-30\piight)ight=2^{60}\left(\cos0+i\sin0ight)

    Запишем результат в экспоненциальной форме:

    ho\left(\cos\phi+i\sin\phiight)=ho e^{i\phi}

    z^{40}=2^{60}e^{0i}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years