-
Помогите решить уравнение с факториалами. Пожалуйста, срочно((
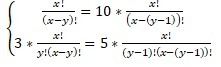
-
Предмет:
Алгебра -
Автор:
addisondunlap - 6 лет назад
-
Ответы 1
-
-
Автор:
kissyuxqs - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОЧНО составить 3-5 вопросов к предложению
Nemo travelled underwater on a submarine
Заранее спасибо-
Предмет:
Английский язык -
Автор:
bradyqn8e - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Как решить x(-2x+6)=0
-
Предмет:
Алгебра -
Автор:
tabethafvmy - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Сколько километров приодолевает гепард
-
Предмет:
Биология -
Автор:
weinerjlir - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Построить изображение предмета, прошедшего через собирающую линзу
-
Предмет:
Математика -
Автор:
teófaneskw3k - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
