-
Вычислите определённый интеграл методом интегрирования по частям
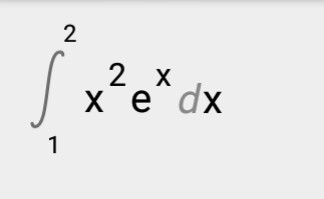
-
Предмет:
Алгебра -
Автор:
skinny minny - 6 лет назад
-
Ответы 1
-
Найдем неопределенный интеграл
-
Автор:
buffie - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Адамның хал-ахуалын жақсартуға бағытталған іс-шаралар туралы нұсқаулық жаз.
-
Предмет:
Қазақ тiлi -
Автор:
cowboymqhk - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
100 баллов! Поставьте слова в скобках в правильные формы:
Если можете объяснить почему, тогда буду крайне благодарен
1) Here ..... (come) the bus.
2) Here .... (come) Mum and Dad!
3) Whe ..... (you/shout) at me so loudly? ..... (you/suspect) me of taking the money from your pursue?-
Предмет:
Английский язык -
Автор:
matildedv1v - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Отец старше сына на 26 лет,а вместе им сейчас 42 года. Сколько лет сыну??
-
Предмет:
Математика -
Автор:
mombodkirp - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
простейшие которые вызывают болезни у людей
-
Предмет:
Биология -
Автор:
picassodonovan - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
