Задать вопрос Регистрация
Помочь другим

  • предел последовательности, помогите пожалуйста..номер 6 и 7

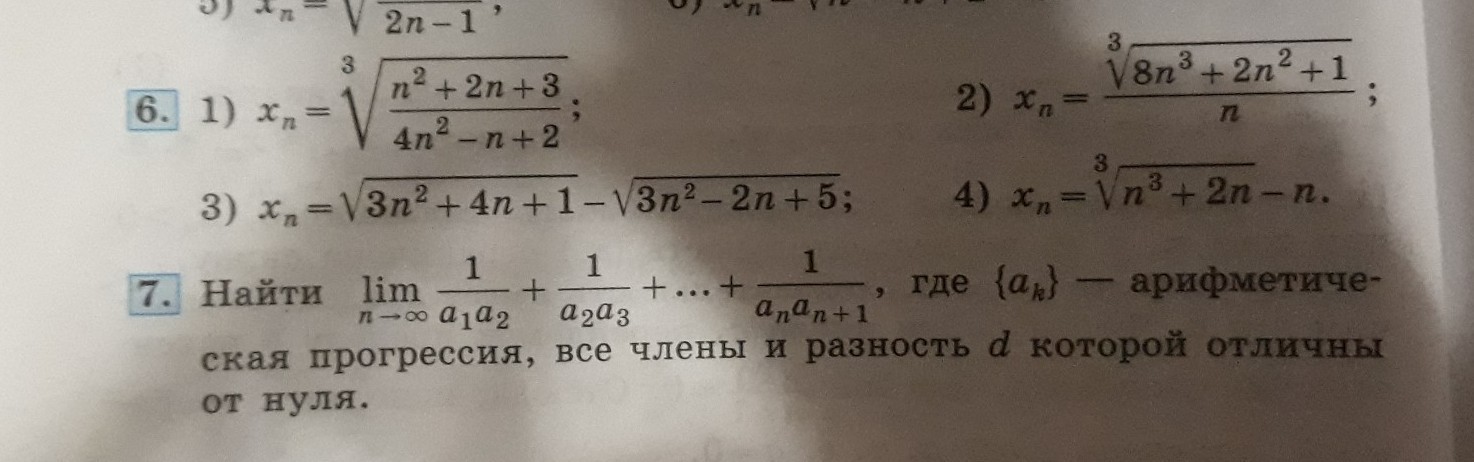
    question img

Ответы 1

  • На счет 6 примера - не указано условие... Не гарантировано точность условии

    \displaystyle \frac{1}{a_1a_2}+\frac{1}{a_2a_3}+...+\frac{1}{a_na_{n+1}}=\frac{1}{a_1(a_1+d)}+\frac{1}{(a_1+d)(a_1+2d)}+...+\\ \\ +\frac{1}{(a_1+(n-1)d)(a_1+nd)}=-\frac{1}{d}\bigg(\frac{-d}{a_1(a_1+d)}+\frac{-d}{(a_1+d)(a_1+2d)}+...+\\ \\+\frac{-d}{(a_1+(n-1)d)(a_1+nd)}\bigg)=-\frac{1}{d}\bigg(\frac{a_1-(a_1+d)}{a_1(a_1+d)}+\frac{a_1+d-(a_1+2d)}{(a_1+d)(a_1+2d)}+\\ \\ +...+\frac{a_1+(n-1)d-(a_1+nd)}{(a_1+(n-1)d)(a_1+nd)}\bigg)=-\frac{1}{d}\bigg(\frac{1}{a_1+d}-\frac{1}{a_1}+\frac{1}{a_1+2d}-

    \displaystyle -\frac{1}{a_1+d}+...+\frac{1}{a_1+nd}-\frac{1}{a_1+(n-1)d}\bigg)=-\frac{1}{d}\bigg(-\frac{1}{a_1}-\frac{1}{a_1+(n-1)d}\bigg)

    Посчитаем предел :)

    \displaystyle\lim_{n \to \infty}-\frac{1}{d}\bigg(-\frac{1}{a_1}-\underbrace{\frac{1}{a_1+(n-1)d}}_{=0}\bigg)=\bigg(-\frac{1}{d}\bigg)\cdot \bigg(-\frac{1}{a_1}\bigg)=\frac{1}{a_1d}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years