-
Пожалуйста мне очень нужна ваша помощь,срочно нужно решение,всё на картинке
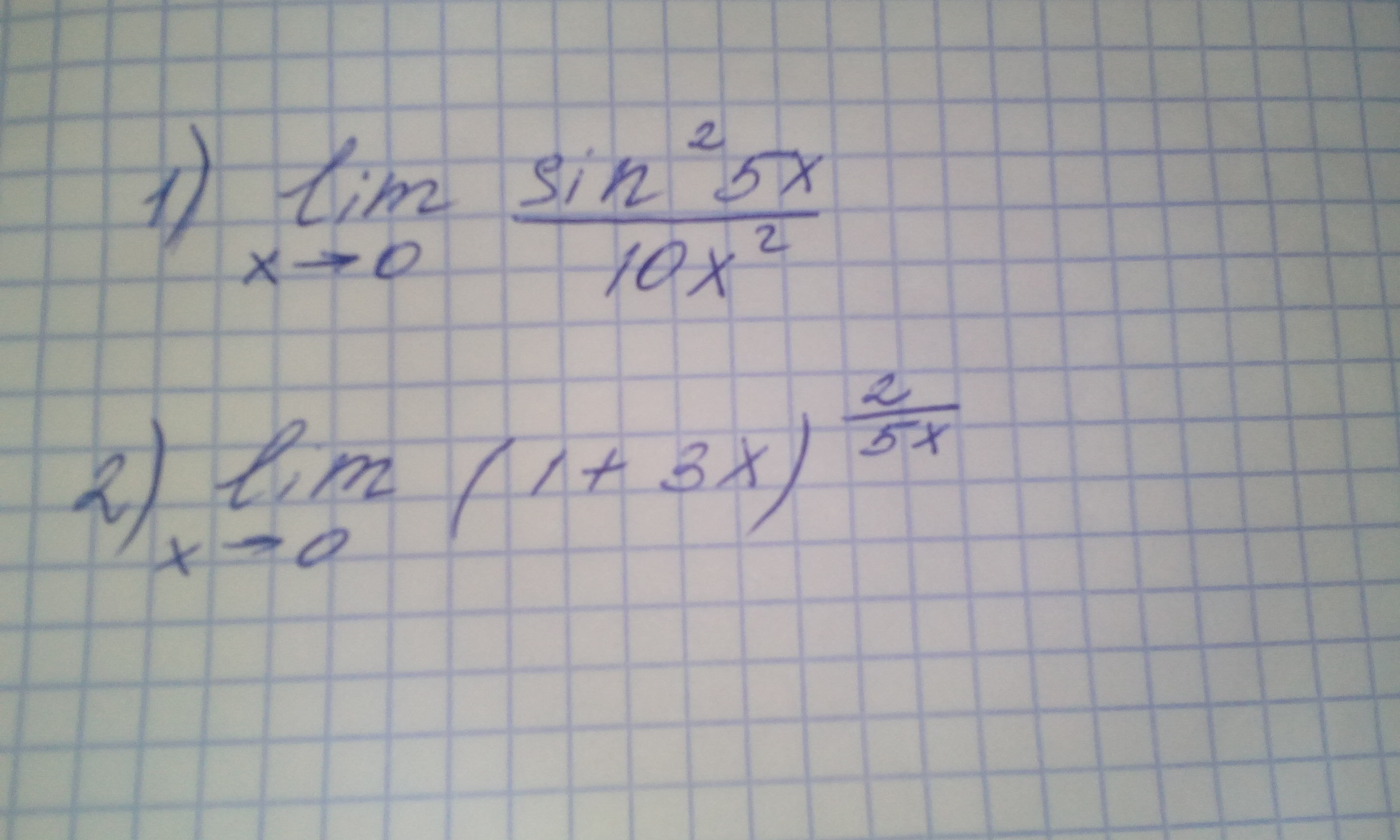
Ответы 2
Еще вопросы
-
Заполните таблицу №4
Пожалуйста!
Мне нужно срочно! -
Вопрос???
1) Что значит <<общественное мнение>> и какое значение оно имеет в жизни общества?
2) Что вы знаете о нашем обществе, его традициях, обычаях и законах-
Предмет:
Математика -
Автор:
aurorabarrett - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
помогите пожалуйста сделать 5 вопросов на английском с переводом на русский
-
Предмет:
Английский язык -
Автор:
vidal - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- Может ли тело находясь в покое относительно Земли, двигаться относительно других? Если может то почему!???
How much to ban the user?
1 hour
1 day
100 years
