Задать вопрос Регистрация
Помочь другим

  • Найти неопределенные интегралы, используя замену переменой или подведение функции под знак дифференциала:

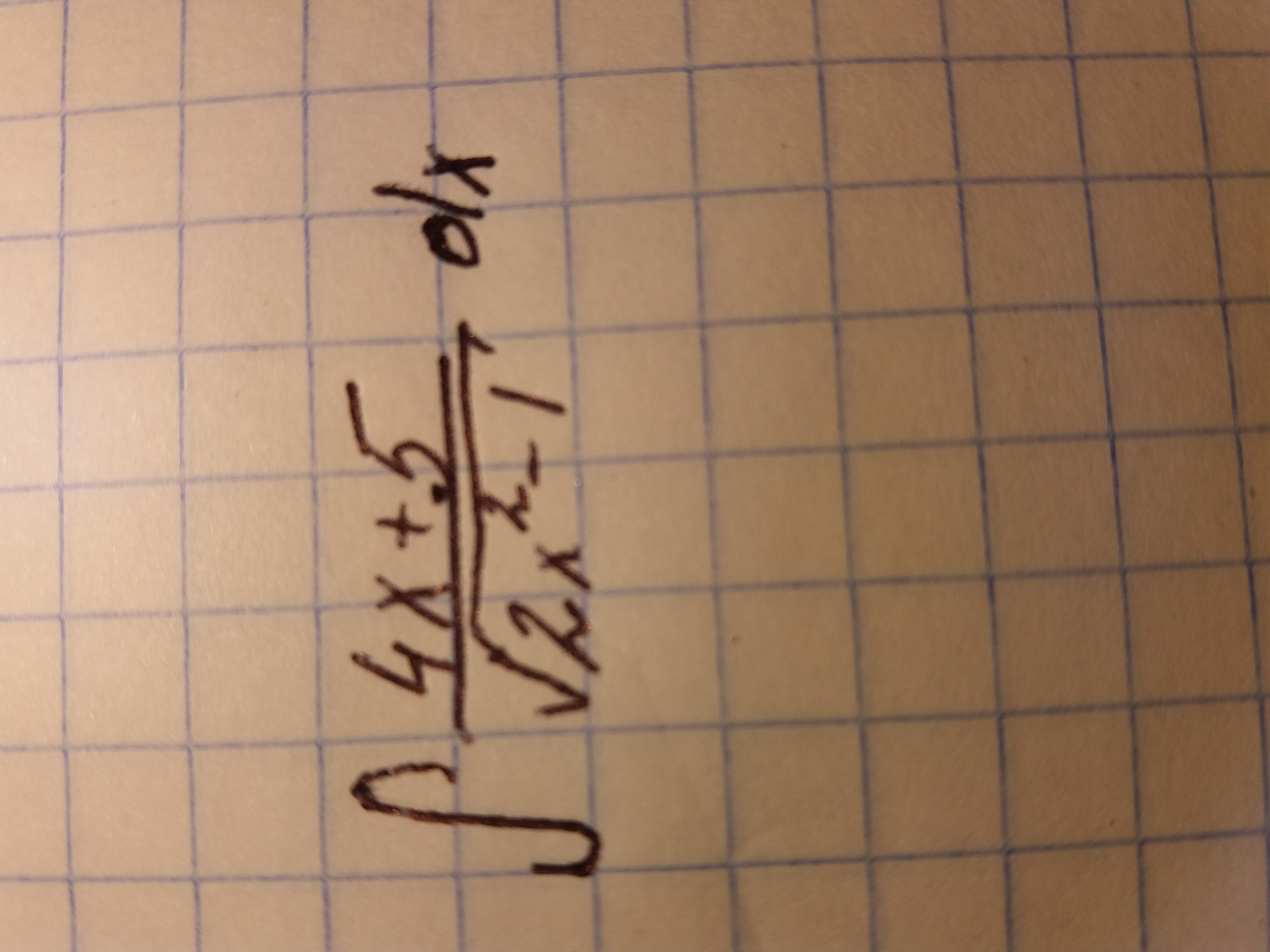
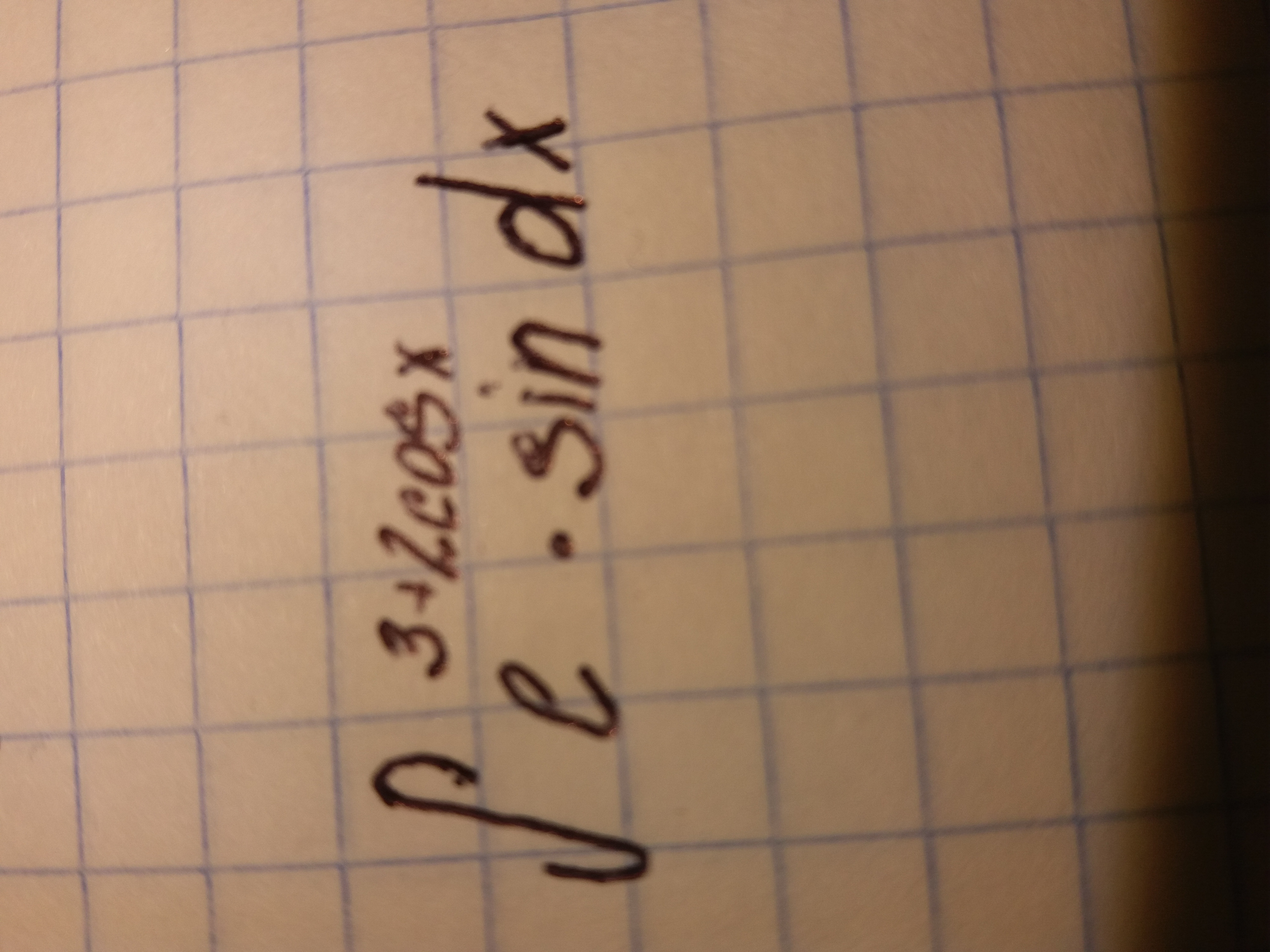
    question img
    question img

Ответы 2

  • Будьте добры, помогите с https://znanija.com/task/30200913

    • Автор:

      george92
    • 6 лет назад
    • 0

  • 1)\; \; \int \frac{4x+5}{\sqrt{2x^2-1}}\, dx=\int \frac{4x\, dx}{\sqrt{2x^2-1}}+\int \frac{5\, dx}{\sqrt{2x^2-1}}=\Big [\, t=2x^2-1\; ,\; dt=4x\, dx\, \Big ]=\\\\=\int \frac{dt}{\sqrt{t}}+5\cdot \int \frac{dx}{\sqrt{(\sqrt2x)^2-1}}=2\sqrt{t}+5\cdot \frac{1}{\sqrt2}\cdot \int \frac{\sqrt2\, dx}{\sqrt{(\sqrt2x)^2-1}}=\\\\=2\sqrt{t}+\frac{5}{\sqrt2}\cdot \int \frac{d(\sqrt2x)}{\sqrt{(\sqrt2x)^2-1}}=2\sqrt{2x^2-1}+\frac{5}{\sqrt2}\cdot ln|\sqrt2x+\sqrt{(\sqrt2x)^2-1}|+C

    2)\; \; \int e^{3+2cosx}\cdot sinx\, dx=\Big [\, t=3+2cosx\; ,\; dt=-2sinx\, dx\, \Big ]=\\\\=-\frac{1}{2}\cdot \int e^{t}\cdot dt=-\frac{1}{2}\cdot e^{t}+C=-\frac{1}{2}\cdot e^{3+2cosx}+C

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years