-
Помогите, пожалуйста, вычислить предел. Распишите, пожалуйста, все очень подробно.
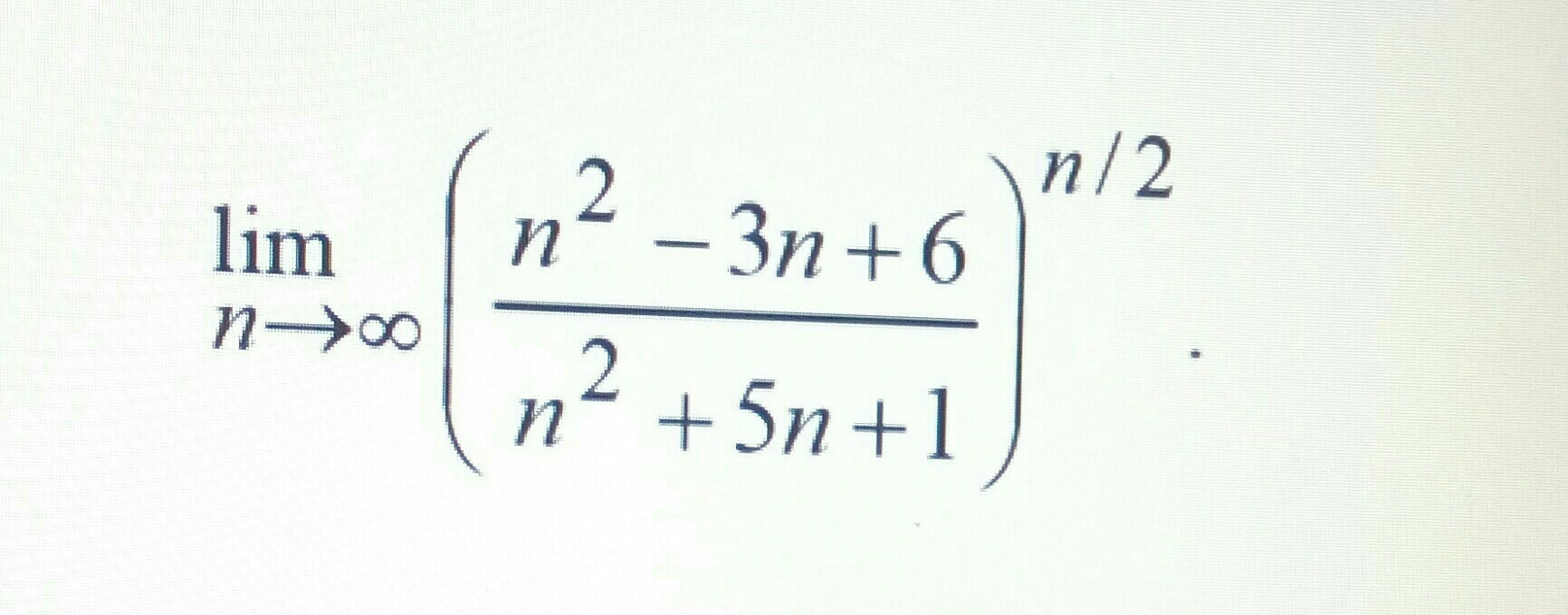
-
Предмет:
Алгебра -
Автор:
amadeoyoung - 6 лет назад
-
Ответы 7
-
Разделите то, что в скобках (одновременно и числитель и знаменатель на x^2). а потом подставьте бесконечность) и получится 1.
-
Автор:
gracetodd - 6 лет назад
-
0
-
-
Или логарифмируя и переходить к произведению в степени. получиться что (∞ *1^{∞-1}) - по правилу лопиталя. одним из множителей второго предела является ∞, что уже говорит о том, что вычислить этот предел невозможно. Таким образом, 1^∞ является неопределённостью, и это доказано.
-
Автор:
aidan7of5 - 6 лет назад
-
0
-
-
Я уже написал выше. ТОЧНОЙ единицы там не будет, мы будем стремится к 1 но не достигать ее. И смотря с какой стороны к 1 приближаемся отсюда и неопределенность.
-
Автор:
averiemclean - 6 лет назад
-
0
-
-
Но е^(-4) приблизительно 0,0183.
-
Автор:
eloise - 6 лет назад
-
0
-
-
так это не неопределённость а ответ)
-
Автор:
chickie7caq - 6 лет назад
-
0
-
-
Поскольку тут неопределённость
, то нужно воспользоваться вторым замечательным пределом
-
Автор:
kayleyrcib - 6 лет назад
-
0
-
-
Тут неопределенность бесконечность на бесконечность.
Если поделим на n^2 то получим неопределенность вида 1 в степени беск
Поработаем с тем что внутри без степени
Поделим и числитель и знаменатель на n^2
Теперь у нас неопределенность 1 в степени беск, это уже лучше, теперь тут 100% второй зам предел
Но нам же нужна единица. Так добавим и вычтем ее.
Так как мне нравится (2) вид заметельного предела, то сделаем замену на
, t стремится к 0 при n стремится к беск
Теперь нам нужно сделать такую же степень и в примере 2 зам предела
- это степень
Сосчитаем предел степени
Ответ:
-
Автор:
tater totvqvu - 6 лет назад
-
0
-
-
Добавить свой ответ
-
чого тугар вовк вбив митька вояка?
-
Предмет:
Литература -
Автор:
calixto - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как в столбик решить пример: 783068 : 13???
-
Предмет:
Математика -
Автор:
highbeamlnmj - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1. экономические решения -
2. касаться, иметь отношение - to
3. экономические ресурсы -
4. качество -
5. данные учета -
6. термины -
7. относиться/касаться/иметь отношение к - to
(you need a preposition here)
8. объязательства/гарантии -
9. деятельность -
Синонимы на Английском-
Предмет:
Английский язык -
Автор:
silky - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- помогите решить, прошу даю 75б. Какой объем углекислого газа может впитать раствор едкого кали объемом 125 мл с массовой долей щелочи 26% и плотностью 1,25 г/мл если образуется кислая соль
