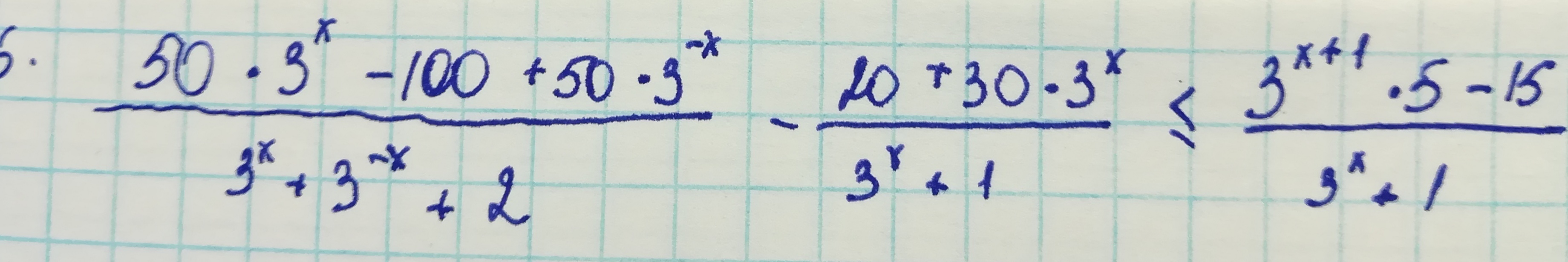Ответы 2
-
К слову, стоило пояснить, что мы имеем право домножать на (t+1)^2/5, т. к. при всех возможных t выражение никогда не обратится в ноль и всегда положительно.
-
Автор:
gregoryfranklin - 6 лет назад
-
0
-
-
Пусть
Проверим левую границу на положительность:
Ответ:
-
Автор:
willow23 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
знайдіть периметр ромба,якщо його сторона утворює з діагоналлю кут 60 і менша діагональ ромба дорівнює 6,5 см.Помогите
-
Предмет:
Геометрия -
Автор:
cutie piemwxn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В один стакан вмещается 150 г семечек.Сколько граммов семечек войдёт в 4 стакана
-
Предмет:
Математика -
Автор:
ferrisrobbins - 6 лет назад
-
Ответов:
8 -
Смотреть
-
-
Во сколько раз 1кг больше 1 мг ?
-
Предмет:
Математика -
Автор:
nathanael - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
(⊙_⊙)СРОЧНО!!!РЕШИТЕ ДЗ .20БАЛОВ,СПАСИБО ,РЕШИТЕ ПРАВЕЛЬНО.!только задание сверху.
-
Предмет:
Алгебра -
Автор:
guillermo53 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years