3√(2+√5)+3√(2-√5) Распешите пожалуйста подробно, с обяснениями, очень нужна помошь,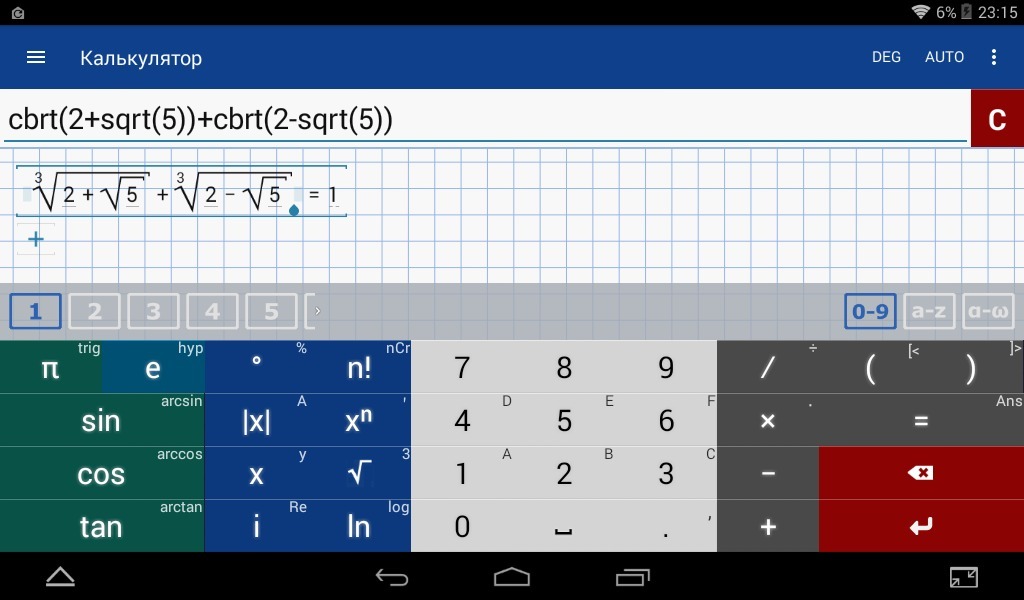

Ответы 3

Помогите пожалуйста сор номер 1 2четверть 7 класс по Алгебре
- Автор:
  aaden178
- 5 лет назад
- 0
$\sf...=\sqrt[\sf 3]{\sf (0.5+0.5\sqrt{5})^3}+\sqrt[\sf 3]{\sf (0.5-0.5\sqrt{5})^3}=0.5+0.5\sqrt{5}+0.5-0.5\sqrt{5}=1$
- Автор:
  snuggles34
- 5 лет назад
- 0
Это нужно доказать: $\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}=1;\ x=\sqrt[3]{2+\sqrt{5}};\ y=\sqrt[3]{2-\sqrt{5}};$
x+y=1; - для упрощение доказываем это.
$x^3+y^3=\sqrt[3]{2+\sqrt{5}}^3+\sqrt[3]{2-\sqrt{5}}^3=2+\sqrt{5}+2-\sqrt{5}=4;$
x³+y³=(x+y)(x²-xy+y²)=(x+y)(x²+2xy+y²-3xy)=(x+y)((x+y)²-3xy)=4;
$xy=\sqrt[3]{2+\sqrt{5}}*\sqrt[3]{2-\sqrt{5}}=\sqrt[3]{2^2-\sqrt{5}^2}=\sqrt[3]{-1}=-1;$
x³+y³=(x+y)((x+y)²-3(-1))=(x+y)((x+y)²+3)=4;
(x+y)³+3(x+y)-4=0; Пусть z=x+y;
z³+3z-4=0; найдем корни.
z³-z²+z²-z+4z-4=0;
z²(z-1)+z(z-1)+4(z-1)=0;
(z-1)(z²+z+4)=0; z=1; первый корень уравнения.
z²+z+4=0; D=1-4*4=-15<0; больше действительных корней нет.
$z=1=x+y=\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}};\\\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}=1;$
что и требовалось доказать.
- Автор:
  wayneua1l
- 5 лет назад
- 0
Добавить свой ответ