-
Решите, пожалуйста!
Заранее благодарю!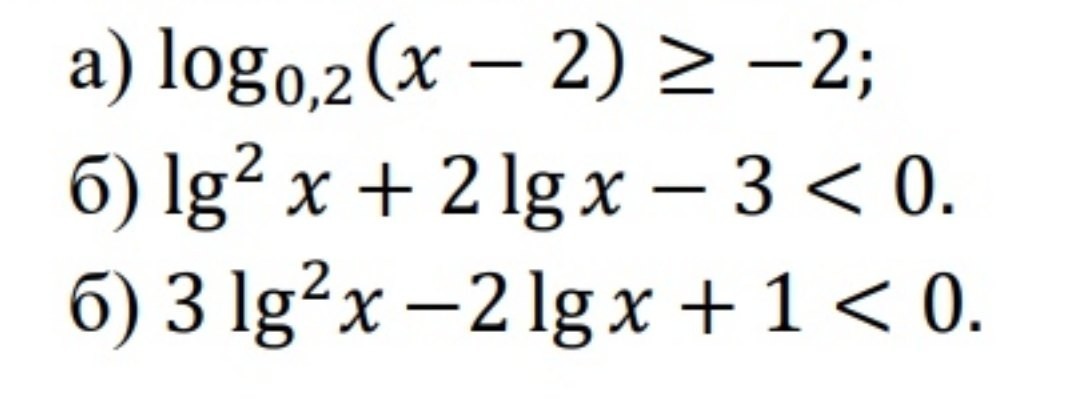
-
Предмет:
Алгебра -
Автор:
estebanv5it - 6 лет назад
-
Ответы 4
-
Тык, а откуда 25 в первом?
-
Автор:
juvenalbowman - 6 лет назад
-
0
-
-
Я всё понял! Спасибо тебе большое!
-
Автор:
leilani - 6 лет назад
-
0
-
-
Я потратили на тебя целый листочек,с тебя листочек))

-
Автор:
raqueldz5c - 6 лет назад
-
0
-
-
а)
Находим ОДЗ:
1)Найти все значения x,при которые дают отрицательный аргумент логарифма:
x-2≤0;
2)Решить неравенство относительно x:
x≤2;
3)Чтобы найти ОДЗ,нужно удалить исключённые значения:
, x>2.
Для 0<a<1 выражение
равно
:
x-2≤0,2⁻²;
Преобразовать десятичную дробь в обыкновенную:
x-2≤
;
Выразить с положительным показателем, используя формулу
:
x-2≤5²;
Вычислить степень:
x-2≤25;
Перенести постоянную в правую часть и сменить её знак:
x≤25+2;
Сложить числа:
x≤27, x>2;
Найти пересечение множества решений и области допустимых значений:
x∈(2;27]
б)
Найти ОДЗ:
1)Найти все значения x, при которые дают отрицательный аргумент логарифма:
x≤0
x≤0;
2)Удалить повторяющееся неравенство:
x≤0;
3)Чтобы найти ОДЗ, нужно удалить исключённые значения:
;
Решить неравенство, используя подстановку t=lgx:
t²+2t-3<0;
Решить неравенство относительно t:
t∈(-3;1);
Сделать обратную подстановку t=lgx:
lgx∈(-3;1);
Записать интервал в виде неравенства:
;
Решить неравенство относительно x:
;
Найти пересечение:
x∈(
;10), x>0;
Найти пересечение множества решений и ОДЗ:
x∈(
;10)
в)
Найти ОДЗ:
1)Найти все значения x, при которые дают отрицательный аргумент логарифма:
x≤0
x≤0;
2)Удалить повторяющееся неравенство:
x≤0;
3)Чтобы найти ОДЗ, нужно удалить исключённые значения:
;
Решить неравенство, используя подстановку t=lgx:
3t²-2t+1<0;
Решить неравенство относительно t:
t∈∅;
Поскольку 3t²-2t+1<0 не имеет решений, исходное уравнение не имеет решений:
x∈∅

-
Автор:
moriahharding - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Выберите выражение, которое неверно показывают сумму единиц слагаемых 427 и 38
a) 1 десяток 5 единиц б) 10+5 в) 10+6
г) 15-
Предмет:
Математика -
Автор:
murphy24 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1784÷8×7-345
Помогите пж не могу решить один дома-
Предмет:
Математика -
Автор:
moniquelnyj - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
складить по одному реченню зи словом неволя и сполукою не воля
-
Предмет:
Українська мова -
Автор:
kirby - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пжжжжж Аркуш зошита в клітинку що має розміри 20 *16 розрізали на квадратики зі стороною 0,5см Яку довжину матиме смужка півсантиметра, викладена з цих квадратів
-
Предмет:
Физика -
Автор:
sherleenj2lv - 6 лет назад
-
Ответов:
2 -
Смотреть
-
