-
Помогите пожалуйста решить
1) точки в которой угловой коэффициент касательной равен K.
2)уравнение касательной к графику функцти в точке с абсцичсой x0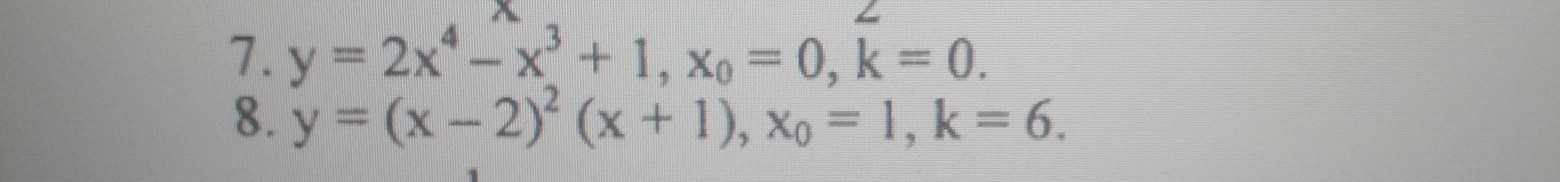
Ответы 1
-
7) Дана функция у = 2х⁴ - х³ + 1.
Её производная равна: y' = 8x³ - 3x² = x²(8x - 3).
Приравняем производную нулю: x²(8x - 3) = 0.
Имеем 2 критические точки: х = 0 и х = (3/8).
В этих точках касательная имеет угловой коэффициент к = 0.
Находим значение функции в этих точках.
х = 0, у = 1. Уравнение касательной у = 1.
х = (3/8), у = (2021/2048). Уравнение касательной у = (2021/2048).
8) Дано уравнение у = (х - 2)²*(х + 1).
Раскроем скобки: у = х³ - 4х² + 4х + х² + 4 = х³ - 3х² + 4.
Её производная равна: y' = 3x² - 6x.
В точке касания угловой коэффициент касательной равен производной.
Приравняем производную заданному значению к: 3x² - 6x = 6.
3x² - 6x - 6 = 0.
Сократим на 3: x² - 2x - 2 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-2)^2-4*1*(-2)=4-4*(-2)=4-(-4*2)=4-(-8)=4+8=12;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√12-(-2))/(2*1)=(√12+2)/2=√12/2+2/2 = (√3 + 1) ≈ 2.732051;
x_2=(-√12-(-2))/(2*1)=(-√12+2)/2=-√12/2+2/2 = (-√3 + 1 ≈ -0.732051.
В этих точках касательная имеет угловой коэффициент к = 6.
Находим значение функции в этих точках.
х = (-√3 + 1), у = 2.
Уравнение касательной у = 2 + 6(х + √3 - 1) = 6х + 6√3 - 4.
х = (√3 + 1), у = 2.
Уравнение касательной у = 2 + 6(х - √3 - 1) = 6х - 6√3 - 4.
-
Автор:
filly fally8sky - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Здравствуйте,помогите определить падеж существительных
-
Предмет:
Русский язык -
Автор:
trevon7ucr - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Q - m/M * R Δ *t ФОРМУЛА ЧЕГО?
-
Предмет:
Физика -
Автор:
emmanuelcrawford - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Формальне Есе на тему "Шкідливість алкоголю і куріння для молодого поколоня"
-
Предмет:
Українська мова -
Автор:
levi22 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
розібрать за будовою слово лісовий
-
Предмет:
Українська мова -
Автор:
lincoln362 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
