Задать вопрос Регистрация
Помочь другим

  • Здраствуйте обясните пожалуйста задачу : найти найбольшее значение у уравнении 12cosA+5sinA-7

    Также зачем мы вынесли √(12^2+5^2)
    И замем здесь "фи"... : (ф=arccos(5:13)...
    Помогите пожалуйста

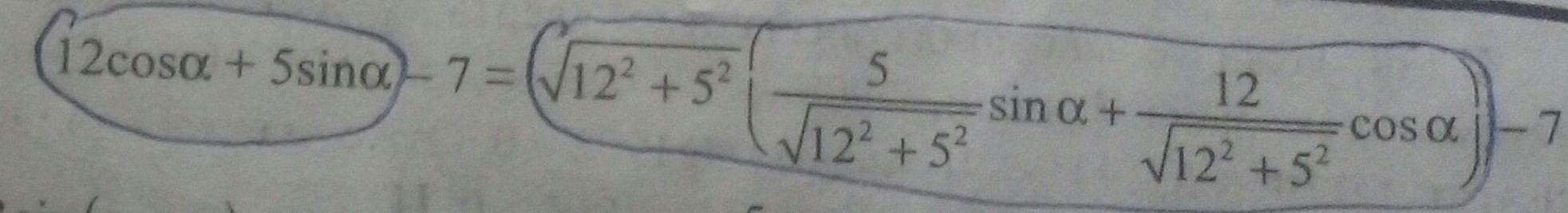
    question img
    question img
    question img

Ответы 1

  • Здесь собственно говоря вам нужно почитать об одной известной формуле: "формула дополнительного угла". Сама формула:

    a \sin (kx)\pm b\cos(kx)=\sqrt{a^2+b^2}\sin(kx\pm\arcsin\frac{b}{\sqrt{a^2+b^2}})

    Ваш ответ на вопрос: "Зачем мы вынести √(12^2+5^2)". Это для того, чтобы свести к синусу суммы двух углов, что собственно упростит нам найти наибольшее и наименьшее значения выражения с помощью двойного неравенства.

    5\sin\alpha+12\cos\alpha-7=\sqrt{5^2+12^2}\sin(\alpha+\arcsin\frac{12}{\sqrt{5^2+12^2}})-7=\\ =13\sin (\alpha+\arcsin\frac{12}{13})=13\sin(\alpha+\phi)

    здесь для простоты обозначили \phi=\arcsin\frac{12}{13}.

    Известно, что синус изменяется на промежутке от -1 до 1, и тогда

    -1\leqslant\sin (\alpha+\phi)\leqslant 1\\ -13\leqslant13\sin(\alpha+\phi)\leqslant13~~~\slash -7\\ -20\leqslant13\sin(\alpha+\phi)-7\leqslant6

    Откуда наибольшее значение выражения — 6.

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years