-
Помогите решить неравенство с модулем, пожалуйстааааа
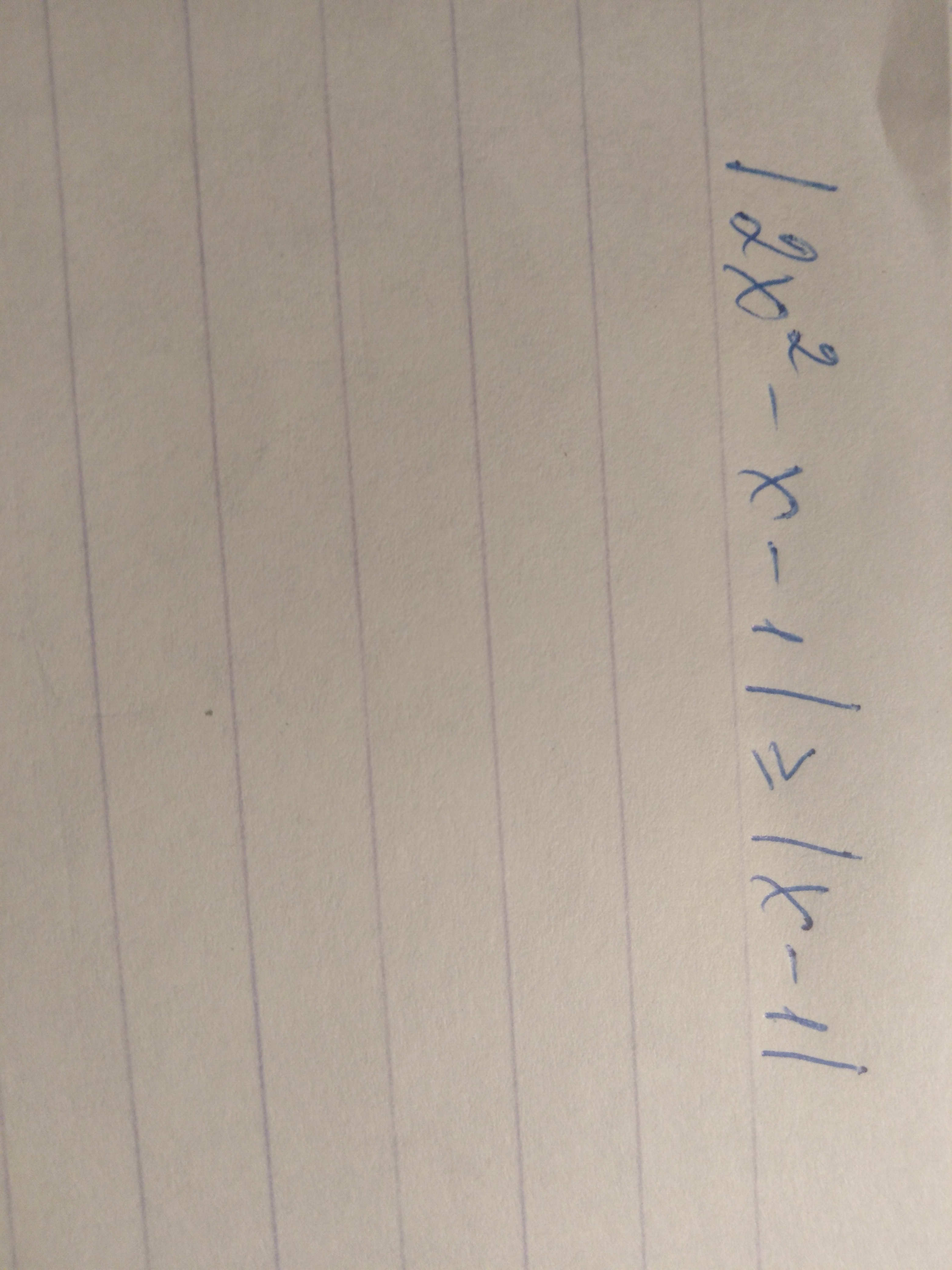
-
Предмет:
Алгебра -
Автор:
rocíosimon - 6 лет назад
-
Ответы 1
-
∣∣2x2−x−1∣∣≥|x−1||2x2-x-1|≥|x-1|Перенесем |x−1||x-1| в левую часть уравнения, вычитая данный член из обеих частей.∣∣2x2−x−1∣∣−|x−1|≥0|2x2-x-1|-|x-1|≥0Прибавим |x−1||x-1| к обеим сторонам уравнения.∣∣2x2−x−1∣∣≥|x−1||2x2-x-1|≥|x-1|Заменим ≥≥ на == в ∣∣2x2−x−1∣∣≥|x−1||2x2-x-1|≥|x-1|.∣∣2x2−x−1∣∣=|x−1||2x2-x-1|=|x-1|Перепишем уравнение с абсолютным значением без знака модуля.(2x2−x−1)=(x−1)(2x2-x-1)=(x-1)(2x2−x−1)=−(x−1)(2x2-x-1)=-(x-1)−(2x2−x−1)=(x−1)-(2x2-x-1)=(x-1)−(2x2−x−1)=−(x−1)-(2x2-x-1)=-(x-1)После упрощения остаются только два уникальных уравнения, которые нам предстоит решить.(2x2−x−1)=(x−1)(2x2-x-1)=(x-1)(2x2−x−1)=−(x−1)(2x2-x-1)=-(x-1)Решим (2x2−x−1)=(x−1)(2x2-x-1)=(x-1) относительно xx.Нажмите, чтобы увидеть больше шагов...x=0;1x=0;1Решим (2x2−x−1)=−(x−1)(2x2-x-1)=-(x-1) относительно xx.Нажмите, чтобы увидеть больше шагов...x=1;−1x=1;-1Запишем все решения.x=0;1;1;−1x=0;1;1;-1Используем каждый корень для создания проверочных интервалов.x≤−1x≤-1−1≤x≤0-1≤x≤00≤x≤10≤x≤1x≥1x≥1Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.Нажмите, чтобы увидеть больше шагов...x≤−1x≤-1 истинно−1≤x≤0-1≤x≤0 ложно0≤x≤10≤x≤1 истинноx≥1x≥1 истинноРешение включает все истинные интервалы.x≤−1or0≤x≤1orx≥1x≤-1or0≤x≤1orx≥1Скомбинируем интервалы.x≤−1x≤-1 или x≥0x≥0.Преобразуем неравенство в интервальный вид.(−∞;−1]∪[0;∞)
-
Автор:
dariusmudl - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- какую роль играет почка
-
Придумать предложения с именами существительными
-
Предмет:
Русский язык -
Автор:
reynaldobird - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
за одни сутки через неплотно закрытый кран со струей толщиной в спичку теряется 400 л воды сколько восмилитровых вёдер по пусто вытекает из этого крана за 30 дней:
решите плиз:3-
Предмет:
Математика -
Автор:
jakepham - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Из чисел 0 1 2 3 4 5 выбери самое большое и самое маленькое составь с выбранными числами две суммы составь три суммы в которых оба слагаемых равны
-
Предмет:
Математика -
Автор:
soxdf0c - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
