Розвязати нерівність: log0.5(x-1)+log0.5(x-2)≥-1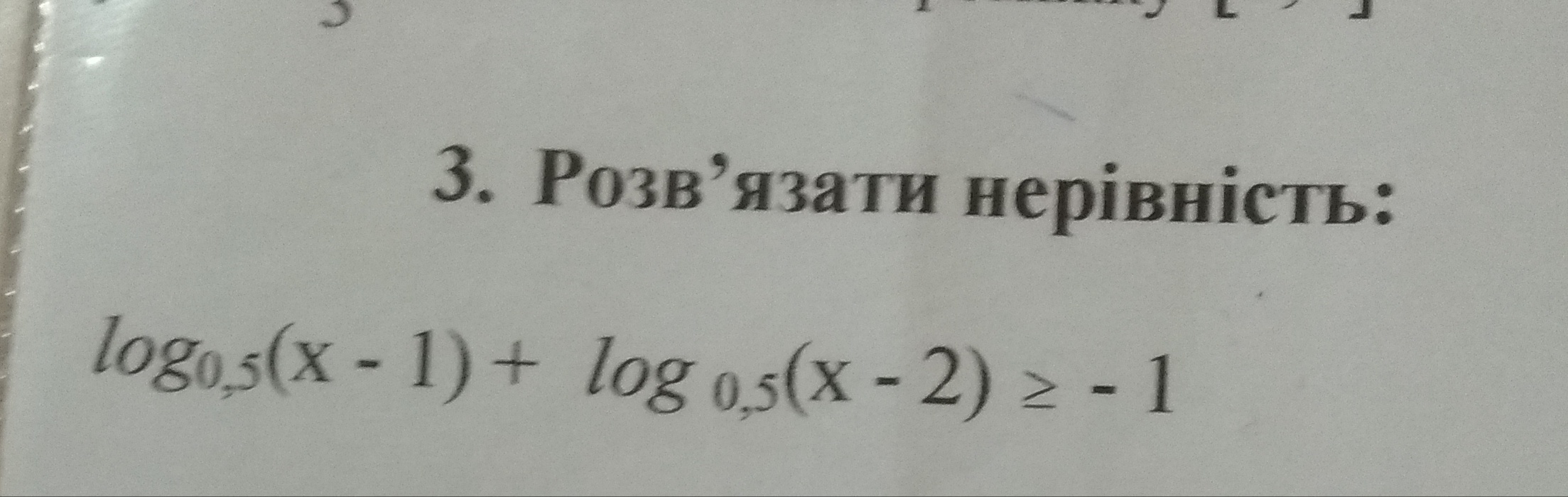

Розвязати нерівність:
log0.5(x-1)+log0.5(x-2)≥-1
- Предмет:
  Алгебра
- Автор:
  dragonflyoupr
- 5 лет назад

Ответы 2

$\log _{0.5}(x-1) + \log _{0.5}(x-2) \ge -1 \\ \\ ODZ: x > 1, \ x > 2 \ ightarrow \ x > 2 \\ \\ \log _{0.5}((x-1)(x-2)) \ge - 1 \\ \\ -\log _{2}(x^{2}-3x+2) \ge - 1 \\ \\ x^{2} - 3x+2 \le 2 \\ \\ x(x-3)\le 0 \\ \\ x \in [0;3]$
С учётом ОДЗ:
$x \in (2;3]$
Ответ: x ∈ (2;3]
- Автор:
  haleywise
- 5 лет назад
- 0
Смотри ......................
- Автор:
  noemilin
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Составить краткую запись для задачи: В магазине имеются лимоны, апельсины и мандарины, всего 740 кг. Если бы продали 55 кг лимонов, 36 кг апельсинов и 34 кг мандаринов, то оставшиеся массы лимонов, апельсинов и мандаринов оказались бы равными. Сколько килограммов фруктов каждого вида имеется в магазине?
- Предмет:
  Математика
- Автор:
  america
- 5 лет назад
- Ответов:
  
  1
- Смотреть
лёгкий тест

1.Любая социальная норма:
А. Является обязательным правилом поведения
Б. обеспечивается силой государства
В. регулирует общественные отношения
Г. выражается в официальной форме
2. Какому виду норм соответствует следующая характеристика: Они закрепляют представление о «добре и зле» в поведении людей?
А. обычаям и традициям Б. моральным нормам
В. правовым нормам Г. эстетическим нормам
3. Правовые нормы в отличие от других социальных норм
А. опираются на силу общественного мнения
Б. обеспечиваются силой государственного принуждения
В. поддерживаются моральным сознанием
Г. осваиваются в процессе социализации
4. К социальным нормам относятся:
А. научные идеи Б. обычаи
В. экономические законы Г. технические нормы
5. Художник следует в своем творчестве сложившимся в данную эпоху представлениям о прекрасном, т.е.
А. традициям Б. этическим нормам
В. эстетическим нормам Г. правилам этикета
6. Верны ли следующие суждения о социальных нормах?
А. Участие родителей в воспитании детей является социальной нормой.
Б. Социальные нормы вырабатываются, как правило, экономической элитой общества.
1) верно только А 2) верно только Б
3) верны оба суждения 4) оба суждения неверны
7. Для характеристики понятия «социальные нормы» используются термины
А. класс, сословие Б. предупреждение, разрешение
В. обучение, образование Г. воображение, мышление
8. Верны ли следующие суждения о социальных нормах?
А. Социальные нормы имеют общий характер, регулируют типичные ситуации и рассчитаны на многократное применение.
Б. Все социальные нормы, как правило, закрепляются в письменных источниках.
1) верно только А 2) верно только Б
3) верны оба суждения 4) оба суждения неверны
9. Учитель на уроке рассказывал о социальных нормах. Сравните нормы права и морали. Выберите и запишите порядковые номера черт сходства, порядковые номера черт отличия.
1) регулируют общественные отношения
2) фиксируются в специальных актах
3) поддерживаются силой государства
4) придают общественному развитию устойчивость
10. Считается, что люди, приехавшие в город Кызыл в Республике Тува, обязательно должны прийти к каменной стелле, расположенной в географическом центре Азии – в месте слияния двух истоков реки Енисей. В этом проявляется действие
А. этикета Б. традиции В. прав Г. морали
11. Что является примером моральной нормы?
А. Перед едой нужно мыть руки.
Б. Безбилетный проезд в общественном транспорте наказывается штрафом.
В. На новоселье первой в квартиру должна зайти кошка.
Г. Свои обещания нужно выполнять.
12 Верны ли следующие суждения о социальных нормах?
А. Выполнение социальных норм обеспечивается исключительно силой общественного мнения.
Б. Социальные нормы регулируют жизнь общества.
1) верно только А 2) верно только Б
3) верны оба суждения 4) оба суждения неверны
13. Составьте предложение, отражающее универсальный характер социальных норм.
14. Мера отрицательного или положительного воздействия на человека - это:
А. социальная норм Б. социальная санкция
В. социальная роль Г. социальный статус
- Предмет:
  Обществознание
- Автор:
  yaelko2s
- 5 лет назад
- Ответов:
  
  1
- Смотреть
Помогите пожалуйста решить 2 вариант, 1) задание под буквой а). Заранее спасибо!
- Предмет:
  Алгебра
- Автор:
  chazwmkw
- 5 лет назад
- Ответов:
  
  1
- Смотреть
Даша вырезала 37 снежинок А Оля на 15 снежинок меньше Сколько снежинок всего вырезали девочки решение
- Предмет:
  Математика
- Автор:
  ricky
- 5 лет назад
- Ответов:
  
  5
- Смотреть

Розвязати нерівність: log0.5(x-1)+log0.5(x-2)≥-1

Ответы 2

Топ пользователей

Розвязати нерівність:
log0.5(x-1)+log0.5(x-2)≥-1