ДАЮ 25 БАЛЛОВ,ПОМОГИТЕ!
Подскажите пожалуйста, как легко устанавливать со­от­вет­ствие между функ­ци­я­ми и их графиками. парабола, прямая и т. д
9класс.Нужно соответствие между рисунками устанавливать,немного не понимаю,очень хочу разобраться,чтобы все на изи выходило

Прежде всего необходимо знать основные функции :

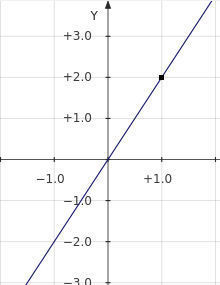
1. Прямая (первая картинка) , общий вид y = kx+b (Например y = 3x-5)

У этой функции нет каких-то особых свойств, тут все просто

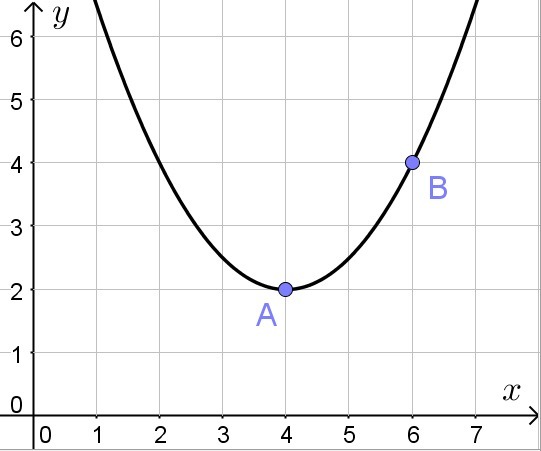
2. Квадратичная функция (вторая картинка) , общий вид y = ax^{2} + bx + c (Например 3x^2-5x+8)

Эта функция полностью зависит от ее коэффициентов , в зависимости от a график будет сжиматься или растягиваться относительно оси Y, в зависимости от b график будет сдвигаться относительно оси X, в зависимости от c график будет сдвигаться относитльно оси Y

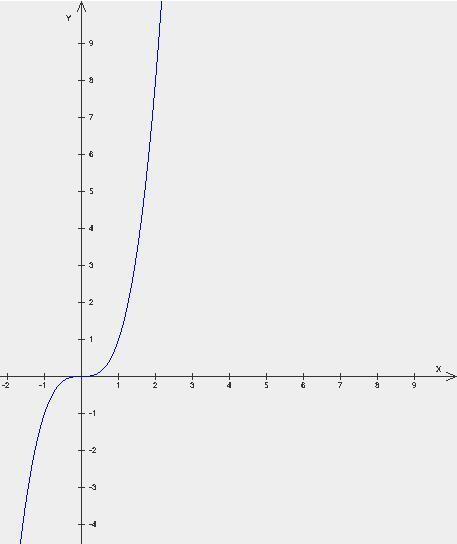
3. Кубическая функция (третья картинка) , общий вид y = ax^{3} + bx^{2} + cx + d (Однако чаще всего в ОГЭ встречается в виде y = x^{3})

Про эту функцию ничего особоенного на уровне ОГЭ знать не надо

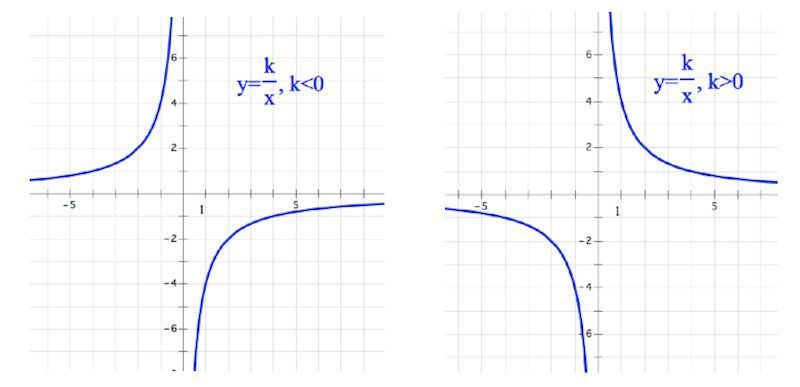
4. Обратная пропорциональность (Четвертая картинка) , общий вид \frac{1}{x}

Очевидно, что x\neq 0 , чем больше X, тем Y меньше, и наоборот, если x больше 0, то график расположен в первой и третьей координатных четвертях, если меньше, то во второй и четвертой

У всех функций есть преобразования :

Например, функция y = x^{2} представляет из себя параболу, а вот y = (x-2)^{2} представляет собой эту же параболу, только сдвинутую относительно оси X на два еденичных отрезка вправо (очевидно y = (x+2)^{2} будет сдвинут влево), то есть F(x+k) представляет собой сдвинутый график F(x) на k отрезков влево или вправо, как описано выше

Еще одно преобразование уже сдвигает график функции относительно оси Y, например y = x^{2} - все та же обычная парабола, а y = x^{2} + 2 представляет из себя ту же параболу, сдвинутую вверх относительно оси Y на два еденичных отрезка вверх(очевидно y = x^{2} - 2 сдвигается вниз), то есть F(x)+k представляет собой сдвинутый график функции F(x) на k отрезков вниз или вверх, как описано выше

Следующее проебразование отражает график функции симметрично относитнльно оси X, например y = x - обычная прямая, но вот y = -x - такой же график, но отраженный относительно оси X, то есть график F(-x) представляет собой симметрично отраженный относительно оси X график функции F(x)

Конечно существует много других преобразований, но как я помню в ОГЭ большего не встречается

Впринципе этого достаточно чтобы быстро определить график любой функции, если конкретнее, то вот алгоритм :

1. По функции определить ее исходную

2. Зная преобразования определить (хотя бы на глаз) коэффиценты преобразования, дальше уже делать выводы