Задать вопрос Регистрация
Помочь другим

  • Обясните пожалуйста решение неравенства методом интервалов, пожалуйста очень подробно
    |2x-1|-|3x+1|≤0
    Должно получится (-∞;-2)U(0;+∞)
    Я пытался но неполучилось...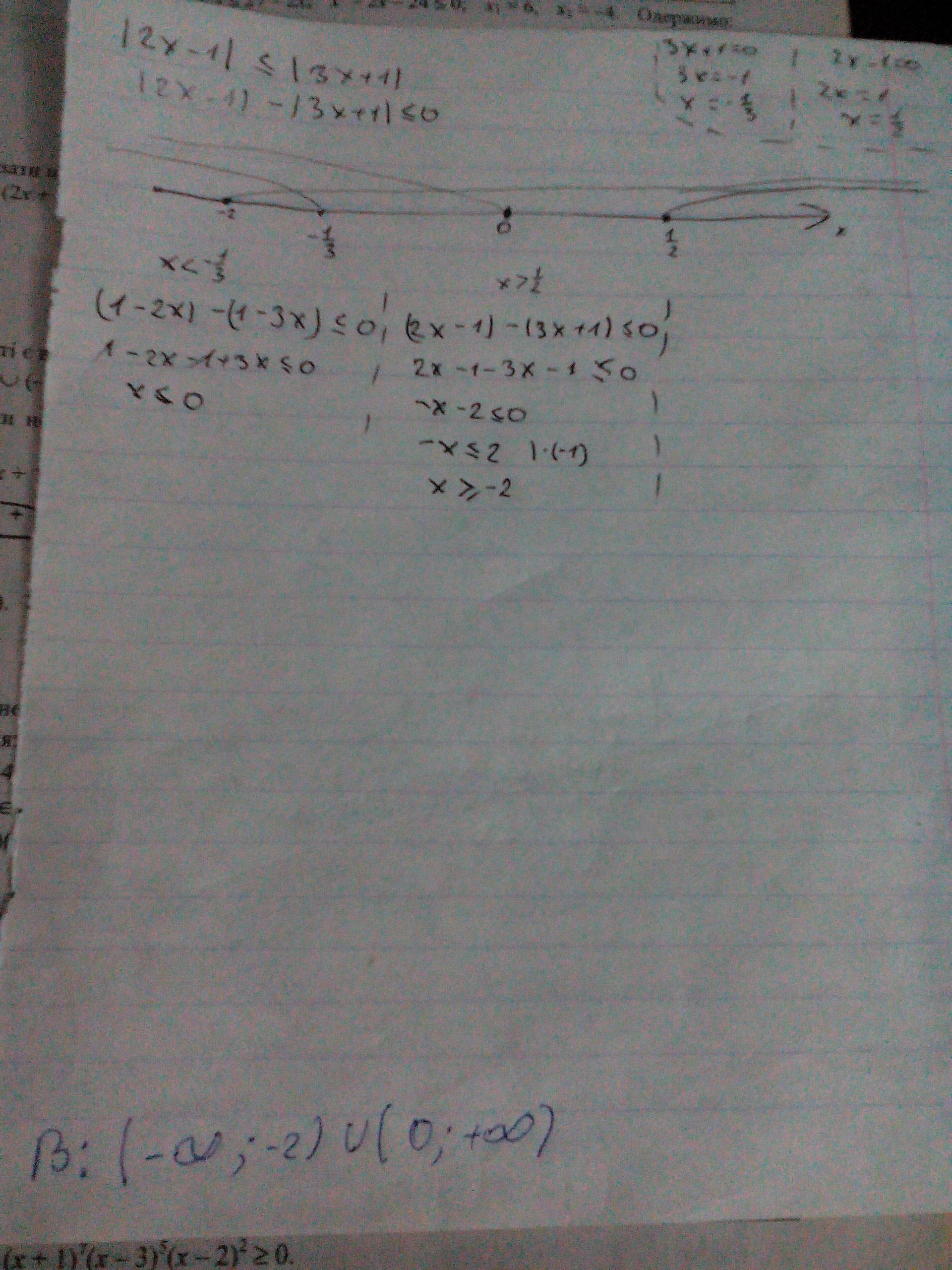

    question img

Ответы 2

  • т.к. обе части неравенства точно неотрицательны (по свойству модуля), то можно возвести обе части неравенства в квадрат и решить обычным методом интервалов. Еще придется применить формулу разности квадратов. Неравенство нестрогое, поэтому точки будут не выколотые.

    |2x-1|\leq |3x+1|\\ \\ (|2x-1|)^2\leq (|3x+1|)^2\\ \\ (2x-1)^2\leq (3x+1)^2\\ \\ (2x-1)^2-(3x+1)^2\leq 0\\ \\ ((2x-1)-(3x+1))*((2x-1)+(3x+1))\leq 0\\ \\ (2x-1-3x-1)*(2x-1+3x+1)\leq 0\\ \\ (-x-2)*5x\leq 0\\ \\ (x+2)*5x\geq 0

          +                           -                          +    

    -----------------  -2  ----------------------0----------------->x

                                        Ответ: (-∞; -2] ∪ [0; +∞)

    ____________________________________________

  • Вы начали верно, рисунок, три участка. Далее нужно было правильно раскрыть модуль. Решение задания приложено.

    answer img

    • Автор:

      jaronvcmo
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years