-
Помогите, пожалуйста, найти производные. Очень подробно.
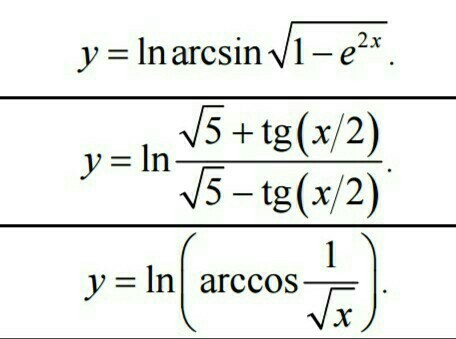
-
Предмет:
Алгебра -
Автор:
champberry - 6 лет назад
-
Ответы 6
-
а втором примере не должно быть просто 5, а не √5?
-
Автор:
lucianofr20 - 6 лет назад
-
0
-
-
а во втором*
-
Автор:
henderson - 6 лет назад
-
0
-
-
В ответе
-
Автор:
margaritafv7q - 6 лет назад
-
0
-
-
В числителе корень из 5, а в знаменателе - просто 5
-
Автор:
scrappyholden - 6 лет назад
-
0
-
-
-
Автор:
hot pepperhhil - 6 лет назад
-
0
-
-
y'=(lnarcsin√(1-e^(2x)))'=1/(arcsin√(1-e^(2x))*(arcsin√(1-e^(2x))'=1/(arcsin√(1-e^(2x)*1/(√1-(1-e^2x)) *(√(1-e^2x)'=1/(srcsin√(1-e^2x)*1/e^x *1/(2√1-e^2x) *(-2e^2x)=1/(arcsin√(1-e^2x) *1/e^x *(-1/(e^2x*√(1-e^2x))
-
Автор:
bobbie - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Сочинение на тему "люби свою семью"
-
Предмет:
Русский язык -
Автор:
robinljnl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сочинение с элементами на тему "Титаник" кратко,когда не прочитал произведение. Срочно пожалуйста.
-
Предмет:
Литература -
Автор:
jordon91 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сочинение-репортаж на любую тему
-
Предмет:
Русский язык -
Автор:
ireneo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите❗️❗️❗️пожалуйста, все олицетворенные примеры из текста
-
Предмет:
Литература -
Автор:
tanner83 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
