Здраствуйте, обясните пожалуйста как решить

Здраствуйте, обясните пожалуйста как решить неравенство...
|x^2-x+1|≥|x^2-3x+4|
Можно ли решить методом интервалов... :)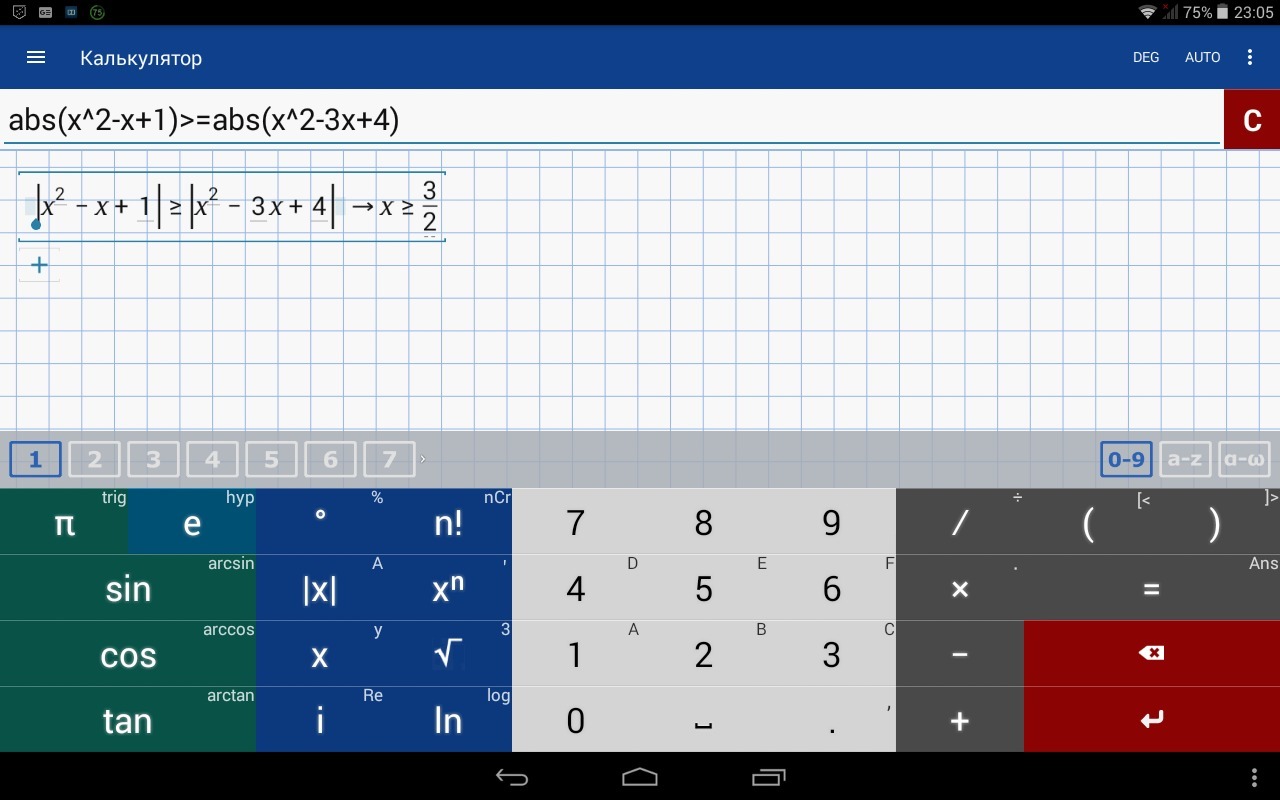
- Предмет:
  Алгебра
- Автор:
  allissonwebster
- 5 лет назад

Ответы 3

как понимать "метод интервалов не имеет нулей" ??? Выразите свою мысль, чтобы понятно было ...
- Автор:
  shyannegtp5
- 5 лет назад
- 0
В етом уравнении нет точек где один из модулей равен 0, по етому мы снимаем модули с обоих уравнений (метод интервалов не имеет нулей)
Получится x^2-x+1≥x^2-3x+4
X≥3/2
- Автор:
  chainam80
- 5 лет назад
- 0
$\boxed {|x|\geq a\; \; \Leftrightarrow \; \; \; \left [ {{x\geq a} \atop {x\leq -a}} ight.}\\\\\\|x^2-x+1|\geq |x^2-3x+4|\; \; \Leftrightarrow \; \; \; \left [ {{x^2-x+1\geq x^2-3x+4\quad } \atop {x^2-x+1\leq -(x^2-3x+4)}} ight.\\\\\left [ {{3x-x\geq 4-1\qquad } \atop {x^2+x^2-x-3x+1+4\leq 0}} ight. \; \left [ {{2x\geq 3\qquad } \atop {2x^2-4x+5\leq 0}} ight. \; \left [ {{x\geq \frac{3}{2}} \atop {x\in \varnothing }} ight.\; \; \; \Rightarrow \; \; x\geq \frac{3}{2}\\\\2x^2-4x+5=0\; ,\; \; D/4=2^2-2\cdot 5=-4-10=-6<0\; \; \Rightarrow$
Уравнение не имеет действительных корней, а квадратный трёхчлен принимает только строго положительные значения, то есть $2x^2-4x+5>0$ . Значит решением неравенства $2x^2-4x+5\leq 0$ будет пустое множество.
Ответ: $x\geq \frac{3}{2}$ .
- Автор:
  mateohanson
- 5 лет назад
- 0
Добавить свой ответ