-
даны числа z1=3-4i z2=-5+7i z3=корень из 3 /2+1/2i найдите модуль и аргумент каждого числа z1+z2;z3-z2;z1*z3 ;z1/z2 подробно пожалуйста
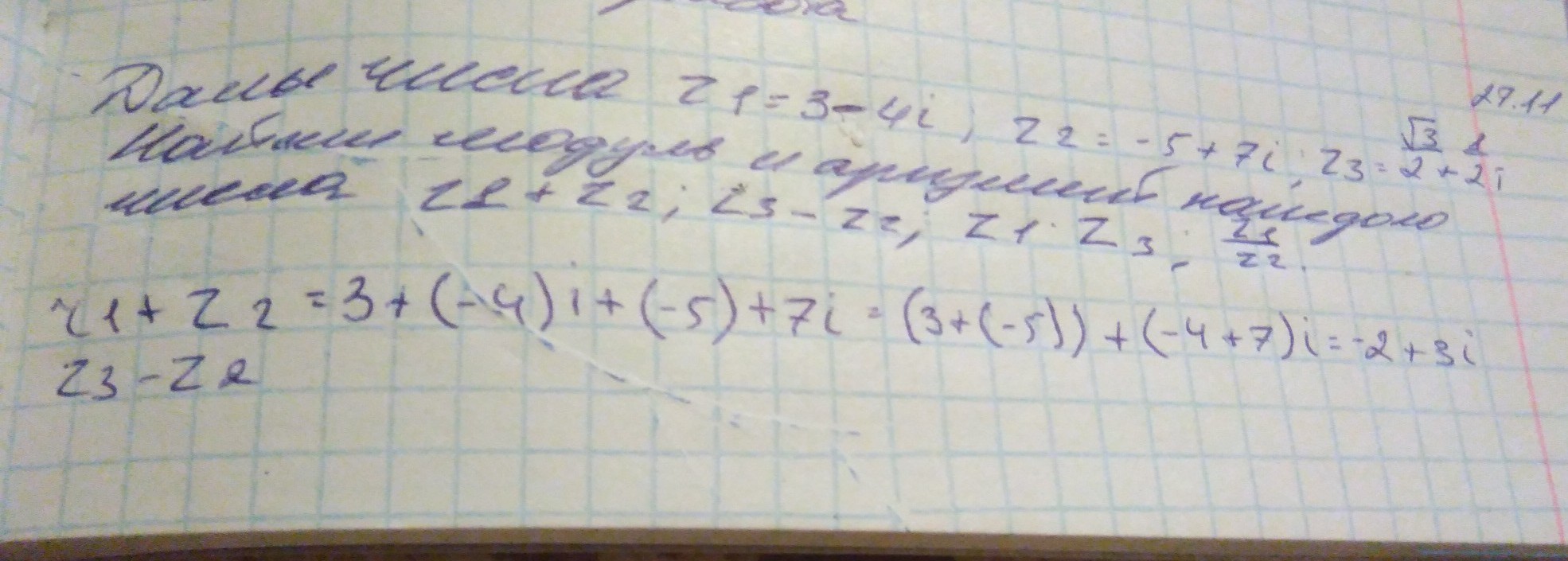
-
Предмет:
Алгебра -
Автор:
conanwalsh - 6 лет назад
-
Ответы 6
-
а рисунок можно пожалуйста
-
Автор:
jett - 6 лет назад
-
0
-
-
какой?
-
Автор:
alipio - 6 лет назад
-
0
-
-
что б найти аргумент и модуль
-
Автор:
bandit42 - 6 лет назад
-
0
-
-
ау
-
Автор:
gloriaberry - 6 лет назад
-
0
-
-
ответь пожалуйста
-
Автор:
hendrix - 6 лет назад
-
0
-
-
Дано:
Найти:
Решение:
1)
(Здесь мы просто сложили уравнение, числа с числами, мнимую единицу с мнимой единицой(в нашем случае "i")
2)
(Здесь просто числитель и знаменатель умножаем на комплексно-сопряженное к знаменателю, можно этого и не делать, ибо и так видно, что ничего не сократится.
3)
(Опять же, просто умножаем и выносим i за скобки.
4)
(Раскрыл скобки, общий знаменатель, всё).
-
Автор:
flashbeps - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
задать формулой прямую пропорциональность график которой параллелен прямой y=7x-2
-
Предмет:
Алгебра -
Автор:
pretty lady - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
словообразование существительных
1) That's a ... (lying) and you know it.
2) His new book examines the United State' ... (involve) in this conflict.
3) One in three marriages end in ... (divorced).
4) Detectives were shocked by the ... (ferocious) of the attack.
5) The work is nearing ... (complete).
6) Her ... (fond) for chocolate was excessive.
7) He turned over in his mind various local ... (occur) which could explain the ... (exist) of this astonishing savage.
8) Our ... (accommodate) wasn't very expensive, and you can stay in a hotel for as little as 30$ a night.
9) He rapidly put into ... (execute) his plan of action.
10) It has been a distasteful and seemingly ruthless ... (do).
11) When I went into her room all her personal ... (belong) had gone.
12) We lit our campfire as ... (dark) fell.
13) The ... (suffer) of the refugees during the war were unbearable.
14) He swore, which was out of ... (characteristic) for him.
15) He completed the job to the best of his ... (enable).
16) It's a ... (quote) from the Bible.
17) You should have seen the ... (dirty) on your car!
18) All the doctors and other medical ... (person) had been working throughout the night.
19) The ... (decisive) is a hammer blow for the coal industry.
20) Wagner calls his program "the worst talk show in America" without a hint of ... (ironic).
21) ... (Predatory) have been observed to avoid attacking brightly coloured species.
22) She feared becoming an object of ... (ridiculous).
23) I think this is a cause for ... (celebrity).
24) Smoking can seriously damage your ... (healthy).
25) The top I percent of the ... (populous) now own 42 percent of the national ... (wealthy).-
Предмет:
Английский язык -
Автор:
chanaesparza - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
WRITE "USEd TO" WHERE POSSIBLE, IF NOT POSSIBLE USE PAST SIMPLE. 1) i/go to the cinema / with my grandparents / every week. 2) we/ not have/ mobile phones or computers 3) my famile/ move/ to san francisco last year 4) i/ get/ a digital watch / for my 7th birthsday 5) i /live/ in that house
-
Предмет:
Английский язык -
Автор:
hooper - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
які особливості сонячного удару?
-
Предмет:
Другие предметы -
Автор:
marc - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
