Задать вопрос Регистрация
Помочь другим

  • Докажите, что данное выражение для всех натуральных значений m и n имеет одно и то же значение.

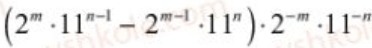
    question img

Ответы 6

  • по английскому
  • NNNLLL54, можете пожалуйста помочь с алгеброй ?

    • Автор:

      kiersten
    • 5 лет назад
    • 0
  • Вопрос на моей странице

    • Автор:

      scott28
    • 5 лет назад
    • 0
  • И желательно с геометрией

    • Автор:

      annalise
    • 5 лет назад
    • 0
  • Заранее спасибо

  • (2^{m}\cdot 11^{n-1}-2^{m-1}\cdot 11^{n})\cdot 2^{-m}\cdot 11^{-n}=\\\\=\Big (\frac{2^{m}\cdot 11^{n}}{11}-\frac{2^{m}\cdot 11^{n}}{2}\Big )\cdot \frac{1}{2^{m}\cdot 11^{n}}=\frac{1}{11}-\frac{1}{2}=-\frac{9}{22}

    Так как мы получили число вне зависимости от того, какие бы значения не принимали переменные m  и  n , то это означает, что заданное выражение для любых натуральных значений m  и  n принимает одно и то же значение.

    • Автор:

      henrysrrc
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years