Подскажите пожалуйста, как решать такие уравнения.. Что надо делать? 8 класс

Подскажите пожалуйста, как решать такие уравнения.. Что надо делать? 8 класс
- Предмет:
  Алгебра
- Автор:
  tysonkrcg
- 6 лет назад

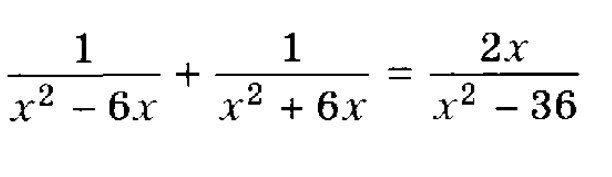
Ответы 4

Блин, точно совсем забыла, спасибо!
- Автор:
  kylanmclean
- 6 лет назад
- 0
Спасибо!)
- Автор:
  lourdesrios
- 6 лет назад
- 0
$\frac{1}{x^{2}-6x }+\frac{1}{x^{2}+6x } =\frac{2x}{x^{2}-36 }\\\\\frac{1}{x(x-6)}+\frac{1}{x(x+6)}-\frac{2x}{(x-6)(x+6)}=0\\\\\frac{x+6+x-6-2x^{2} }{x(x-6)(x+6)}=0\\\\\left \{ {{-2x^{2}+2x=0 }\atop {x(x-6)(x+6)eq0 }} ight.\\\\\left \{ {{x^{2}-x=0 } \atop {xeq 0;xeq-6;xeq6}} ight.\\\\\left \{ {{x(x-1)=0} \atop {xeq0;xeq -6;xeq6}} ight.\\\\x-1=0\\\\x=1$
- Автор:
  nora46
- 6 лет назад
- 0
Перво-наперво ищешь ОДЗ, то есть исключаешь те значения, при которым знаменатель обращается в ноль:
$x^2-36eq 0\\xeq б\sqrt{36} \\xeq =-6;xeq 6;xeq0.$
Затем приводим левую и правую часть к общему знаменателю:
$\frac{1}{x^2-6x} +\frac{1}{x^2+6x} =\frac{2x}{x^2-36} \\\frac{1}{x(x-6)} +\frac{1}{x(x+6)} =\frac{2x}{x^2-36}\\\frac{x+6+x-6}{x(x-6)(x+6)} =\frac{2x^2}{x(x^2-36)}\\\frac{2x}{x(x^2-36)} =\frac{2x^2}{x(x^2-36)}.$
Потом и левую и правую часть умножаем на этот знаменатель, чтобы избавиться от него, далее находим корни получившегося уравнения:
$2x=2x^2\\2x^2-2x=0\\2x(x-1)=0\\x_1=0;x_2=1.$
Возвращаемся к ОДЗ и проверяем, не равняются ли корни уравнения его значениям. Если да, то исключаем их. В нашем случае - это ноль. Исключив его, мы получим 1. Это и есть ответ.
- Автор:
  mckenzie57
- 6 лет назад
- 0
Добавить свой ответ