Задать вопрос Регистрация
Помочь другим

  • Докажите, что значение выражения есть число рациональное:

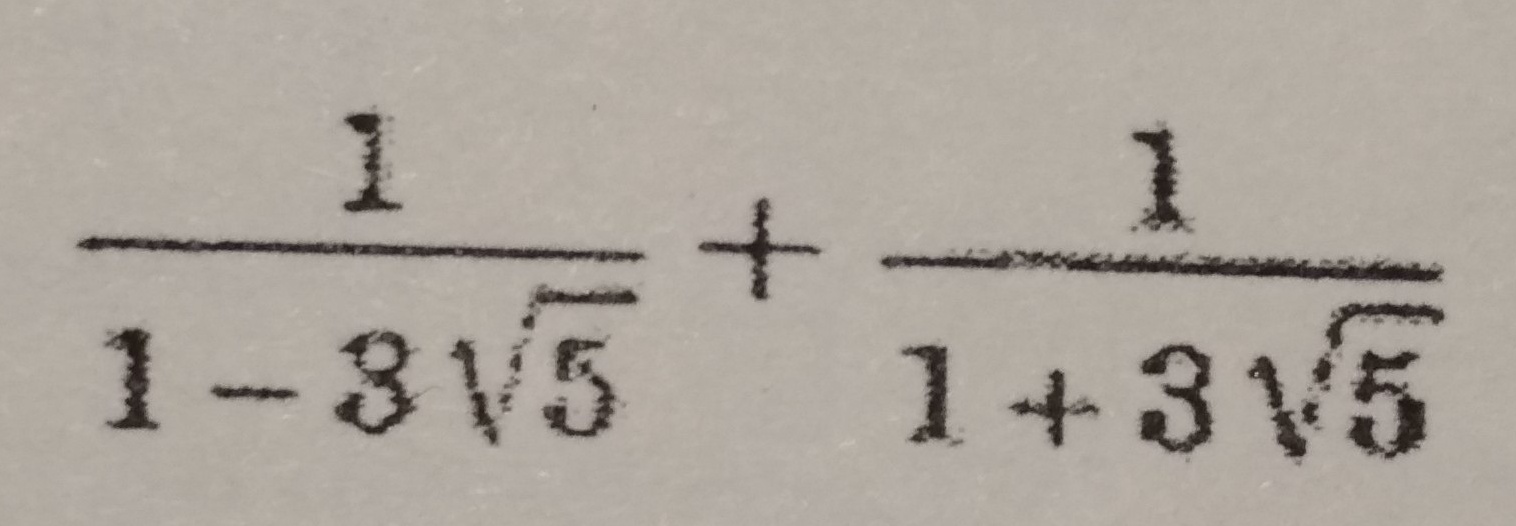
    question img

Ответы 2

  • \frac{1}{1-3\sqrt{5} }+\frac{1}{1+3\sqrt{5} }=\frac{1+3\sqrt{5}+1-3\sqrt{5}}{(1-3\sqrt{5})(1+3\sqrt{5})}=\frac{2}{1^{2} -(3\sqrt{5})^{2}} =\frac{2}{1-45}=-\frac{2}{44}=-\frac{1}{22}

  • Домножим первую дробь на (1+3√5) А вторую на (1-3√5) , чтобы избавиться иррациональности в знаменателе \frac{1 + 3 \sqrt{5} }{(1 - 3 \sqrt{5}){(1 + 3 \sqrt{5} )} } + \frac{1 - 3 \sqrt{5} }{(1 + 3 \sqrt{5})(1 - 3 \sqrt{5} ) } Получили общий знаменатель, который мы свернем в формулу \frac{1 + 3 \sqrt{5} + (1 - 3 \sqrt{5)} }{1 - {3}^{2} \times \sqrt{5} \times \sqrt{5} } = \frac{2}{1 - 9 \times 5} = \frac{2}{ - 44} = - \frac{1}{22} Число рациональное

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years