Задать вопрос Регистрация
Помочь другим

  • Помогите, пожалуйста, вычислить предел, используя правило Лопиталя.

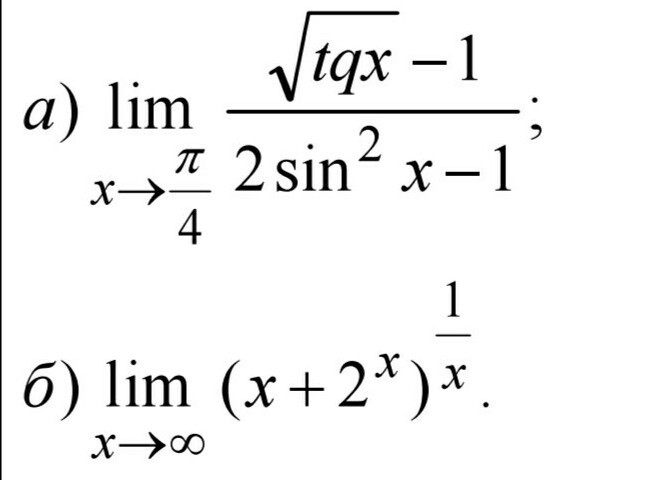
    question img

Ответы 3

  • извините, пожалуйста, а почему во втором примере появилась экспонента?

    • Автор:

      ozzy
    • 5 лет назад
    • 0
  • Чтоб привести выражение к стандартному виду для применения метода Лопиталя

  • \lim_{x \to \frac{\pi }{4}} \frac{\sqrt{tgx}-1}{2sin^2x-1} = \lim_{x \to \frac{\pi }{4}} \frac{\sqrt{tgx}-1}{-cos2x} = \lim_{x \to \frac{\pi }{4}} \frac{(\sqrt{tgx}-1)'}{-(cos2x)'} = \\\lim_{x \to \frac{\pi }{4}} \frac{\frac{1}{2cos^2x\sqrt{tgx}}}{2sin2x} =\lim_{x \to \frac{\pi }{4}} \frac{1}{4sin2xcos^2x\sqrt{tgx}} =\frac{1}{4*1*0,5*1}=\frac{1}{2}

    \lim_{x \to \infty} (x+2^x)^{\frac{1}{x}}= \lim_{x \to \infty} e^{ln(x+2^x)^{\frac{1}{x}}}=\lim_{x \to \infty} e^{\frac{ln(x+2^x)}{x}}}=e^{\lim_{x \to \infty} \frac{ln(x+2^x)}{x}}}=e^{\lim_{x \to \infty} \frac{(ln(x+2^x))'}{x'}}}=e^{\lim_{x \to \infty} \frac{\frac{1+ln2*2^x}{x+2^x}}{1}}}=\\e^{\lim_{x \to \infty} {\frac{(1+ln2*2^x)'}{(x+2^x)'}}}=e^{\lim_{x \to \infty} {\frac{(ln^22*2^x)'}{(1+ln2*2^x)'}}}=e^{\lim_{x \to \infty} {\frac{ln^32*2^x}{ln^22*2^x}}}=e^{ln2}=2

    • Автор:

      calvin
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years