Хелп тригонометрия дайте подсказку или помогите решить.

Хелп тригонометрия дайте подсказку или помогите решить.
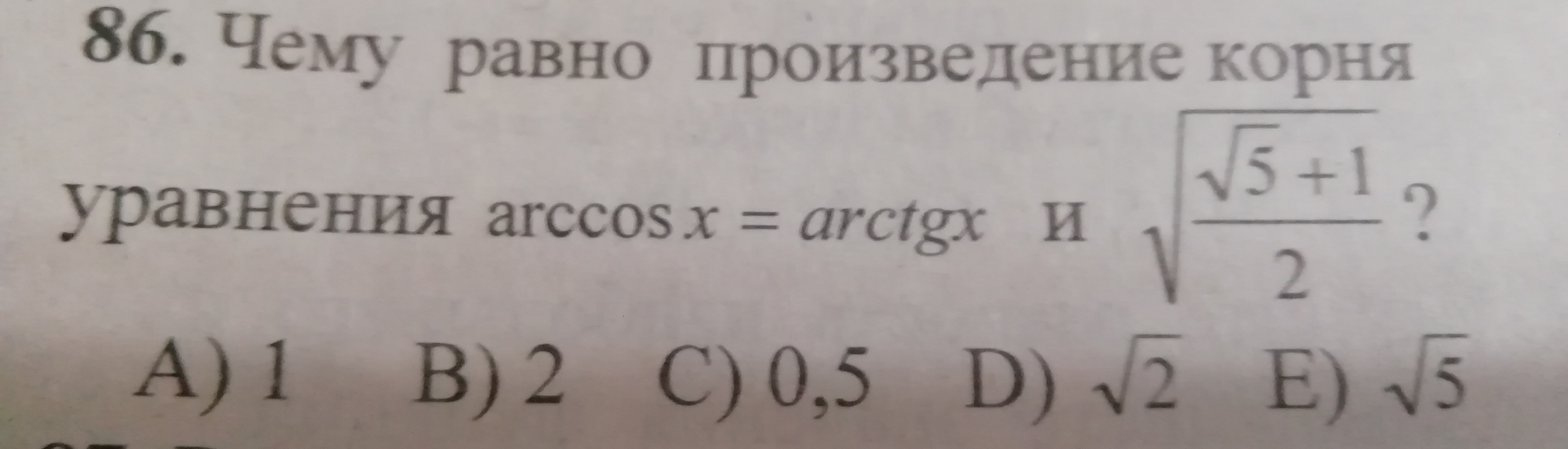
- Предмет:
  Алгебра
- Автор:
  selahschaefer
- 6 лет назад

Ответы 1

Решение. Множество значений арккосинуса есть отрезок [0;π]. Множество значений арктангенса есть интервал (−π/2; π/2). Поэтому если арккосинус равен арктангенсу, то оба они принимаютзначения из промежутка [0; π/2). При этом x может принимать значения из отрезка [−1;1].
Но два числа из промежутка [0; π/2) равны тогда и только тогда, когда равны их косинусы. Поэтому наше уравнение равносильно следующему:
cos(arccosx) = cos(arctgx).
В левой части имеем: cos(arccosx) = x.
В правой части, т.к. $cos^2x=\frac{1}{1+tg^2x}$ (учитывая, что в промежутке [0; π/2) косинус положителен):
cos(arctgx) = $cos(arctgx)=\sqrt{\frac{1}{1+tg^2(arctgx)}}=\sqrt{\frac{1}{1+x^2}}$ .
Получаем уравнение: $x=\sqrt{\frac{1}{1+x^2}}$
Возводим обе части в квадрат и получаем биквадратное
$x^4+x^2-1=0$
Решаем его, учитывая, что x ≥ 0 и получаем $x=\sqrt{\frac{\sqrt{5}-1}{2}}$
Перемножим его с заданным корнем и получим:
$\sqrt{\frac{\sqrt{5}-1}{2}}*\sqrt{\frac{\sqrt{5}+1}{2}}=\sqrt{2}$
- Автор:
  mack20
- 6 лет назад
- 0
Добавить свой ответ

Еще вопросы

Хелп тригонометрия дайте подсказку или помогите решить.

Ответы 1

Топ пользователей