-
Ставлю 30 баллов!!! Ребята пожалуйста решите на листочке подробно !
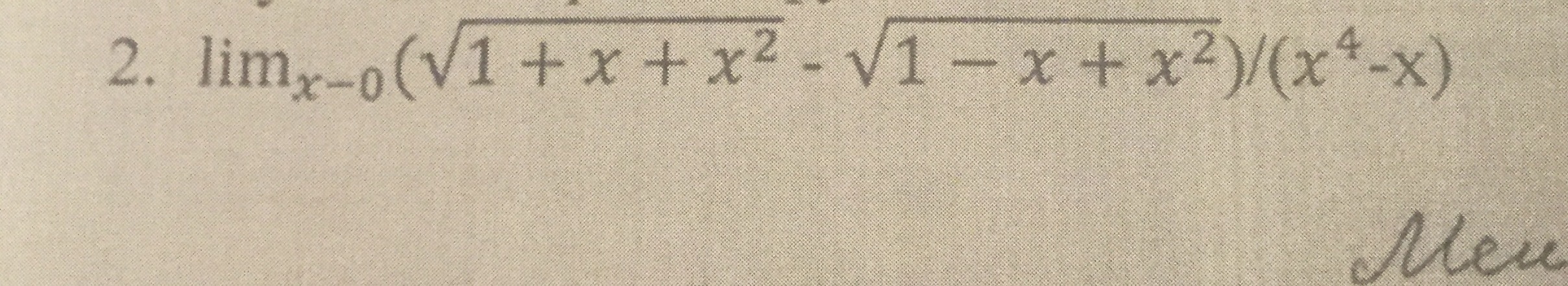
Ответы 2
Еще вопросы
-
(5,26-145,44:48)*11 =
Пожалуйста, очень срочно-
Предмет:
Алгебра -
Автор:
albamartin - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Each of the words in bold is in the wrong sentence. Write a word in bold from another sentence to replace the incorrect one.
1)You should _have_ off that hat because it doesn't look nice.
2)You can _leave_ up your coat in the wardrobe if you like.
3)When my sister and I were young, we would _take_ up in our mother's clothes.
4)My friends are the guys over there who _do_ go suits on.
5)He asked to take her coat, but she decided to _try_ it on.
6)Your shoelaces are not tied and you need to _put_ them up.
7)These trousers are really big, so i think I'll _hang_ a belt on.
8)I'm going to _dress_ on these boots and if i like them, i'll buy them!
СРОЧНО!!!ПОЖАЛУЙСТА!!!ДАЮ 40 БАЛЛОВ!!!ЧЕСТНО!!!-
Предмет:
Английский язык -
Автор:
jessiepatrick - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите пожалуйста перевести. и поставить правильно артикль и прилагательные.
-
Предмет:
Английский язык -
Автор:
emmettcarey - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Make up a sentence: 1)most 2)of the rest 3)evaporates 4)into the air 5)about 6)round 7)water
-
Предмет:
Английский язык -
Автор:
pilar - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
