Задать вопрос Регистрация
Помочь другим

  • требуется выполнить действия вычитания и деления комплексных чисел z1, z2.
    z1 = (-5+i) , z2 = (3+2i).
    - - -
    меня смущает одно , полоска сверху - это отрицание? если да, то когда применять отрицание, после решения или перед ним?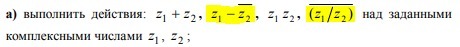

    question img

Ответы 6

  • окончательный ответ 1 - i?

    • Автор:

      yodavzlo
    • 6 лет назад
    • 0
  • поправочка , -1 - i?
  • как я могу с вами связаться? обмен сообщениями недоступен тут говориться.

    • Автор:

      pearlip9k
    • 6 лет назад
    • 0
  • я исправила условие и решение

    • Автор:

      sonia15
    • 6 лет назад
    • 0
  • благодарю.

    • Автор:

      clydezou5
    • 6 лет назад
    • 0

  • z_1=-5+i\; \; ,\; \; z_2=3+2i\; \; \Rightarrow \; \; \overline {z_1}=-5-i\; ,\; \; \overline {z_2}=3-2i\\\\\\z_1+z_2=(-5+i)+(3+2i)=(-5+3)+(i+2i)=-2+3i\\\\\\z_1-\overline {z_2}=(-5+i)-(3-2i)=(-5-3)+(i+2i)=-8+3i\\\\\\z_1\cdot z_2=(-5+i)\cdot (3+2i)=-15-10i+3i+2i^2=\\\\=-15-7i-2=-17-7i\\\\\\\frac{z_1}{z_2}=\frac{-5+i}{3+2i}=\frac{(-5+i)(3-2i)}{(3-2i)(3+2i)}=\frac{-15+10i+3i-2i^2}{3^2-(2i)^2}=\frac{-15+13i+2}{9-4i^2}=\\\\=\frac{-13+13i}{9+4}=\frac{-13+13i}{13}=-\frac{13}{13}+\frac{13}{13}i=-1+i\\\\\overline {(z_1/z_2)}=-1-i

    • Автор:

      alenadkok
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years