Задать вопрос Регистрация
Помочь другим

  • МАТЕМАТИКИ, ПОМОГИТЕ! С НАСТУПИВШИМ! ДАЮ МНОГО БАЛЛОВ

    question img

Ответы 1

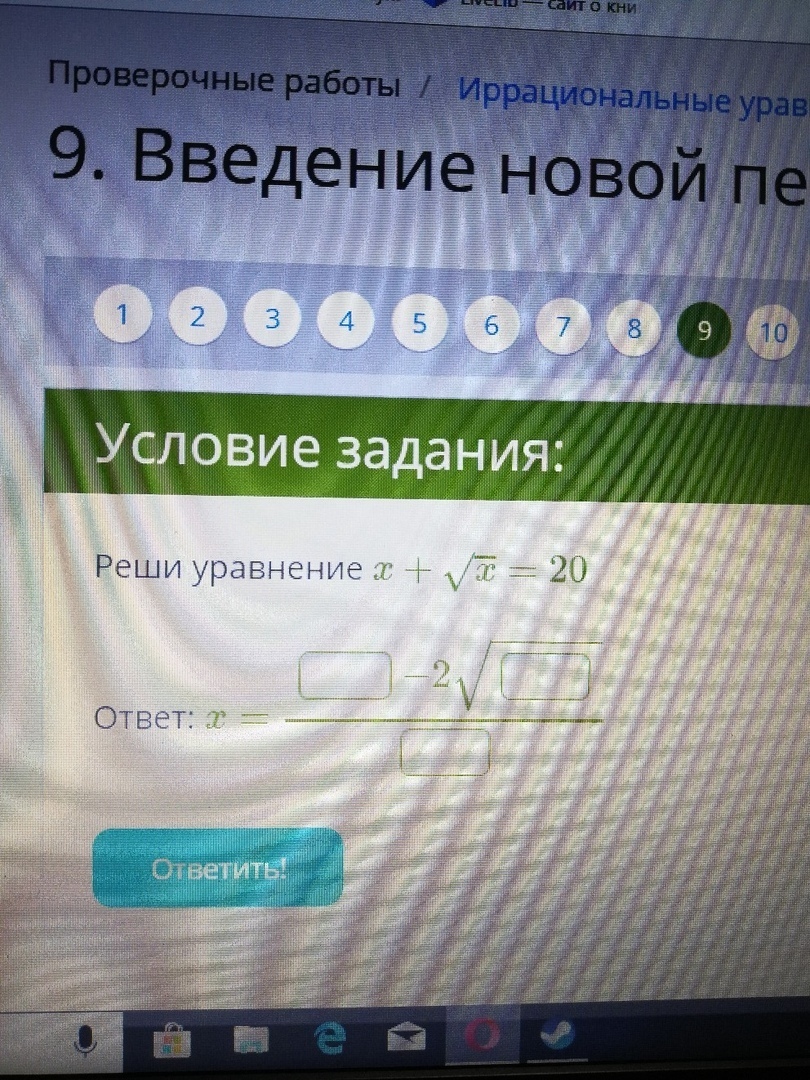
  • Как уже сказали, ответ действительно x=16. Но в окошки не вписывается, поэтому, я думаю, надо в общем виде решить.

    x+\sqrt{x}=\lambda

    Пусть g=\sqrt{x}\Rightarrow g^2=x. Тогда,

    \begin{cases}g^2+g-\lambda=0\,;\smallskip\\g\geq 0\,.\end{cases}\medskip\\\begin{cases}g=\dfrac{-1\pm\sqrt{1+4\lambda}}{2}\,;\smallskip\\g\geq 0\,.\end{cases}

    Получаем, что при \forall\lambda\in\left[-0{,}25\,;+\inftyight) будем иметь \sqrt{4\lambda+1}\geq 0, значит, выпишем условие для \lambda и подходящее значение g.

    \begin{cases}g=\dfrac{-1+\sqrt{4\lambda+1}}{2}\,;\smallskip\\\lambda\geq -0{,}25\,.\end{cases}

    Но g=\sqrt{x}, отсюда

    x=\left(\dfrac{-1+\sqrt{4\lambda+1}}{2}ight)^2;\medskip\\x=\dfrac{4\lambda+2-2\sqrt{4\lambda+1}}{4}\,.

    В данном уравнении \lambda=20 \geq -0{,}25. Значит,

    x=\dfrac{80+2-2\sqrt{80+1}}{4}=\dfrac{82-2\sqrt{81}}{4}

    Что, конечно, равно 16.

    Ответ. x=\dfrac{82-2\sqrt{81}}{4}

    • Автор:

      cline
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years