Задать вопрос Регистрация
Помочь другим

  • Доказать, что ... для любых действительных x и y, имеющих одинаковые знаки

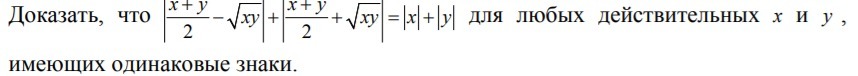
    question img

Ответы 1

  • |x|+|y|= \begin{cases} x+y \ \ \ \ \ x,y>0\\ -x-y\ \ \ x,y<0\end{cases}

    --------------------------

    1) для x,y>0

    \left|\frac{x+y}{2}-\sqrt{xy}}ight| +\left|\frac{x+y}{2}+\sqrt{xy}} ight| =

    \frac{1}{2} \left|x+y-2\sqrt{xy}}ight| + \frac{1}{2} \left|x+y+2\sqrt{xy}} ight| =

    \frac{1}{2} \left|( \sqrt{x}- \sqrt{y} )^2 ight| + \frac{1}{2}\left| ( \sqrt{x}+ \sqrt{y} )^2ight| =

    \frac{1}{2} ( \sqrt{x}- \sqrt{y} )^2 + \frac{1}{2}( \sqrt{x}+ \sqrt{y} )^2 =

    \frac{1}{2} (x-2 \sqrt{xy}+y ) + \frac{1}{2}( x+2\sqrt{xy}+ y )=x+y

    --------------------------

    2) для x,y<0

    \left|\frac{x+y}{2}-\sqrt{xy}}ight| +\left|\frac{x+y}{2}+\sqrt{xy}} ight| =

    \frac{1}{2} \left|x+y-2\sqrt{xy}}ight| + \frac{1}{2} \left|x+y+2\sqrt{xy}} ight| =

    \frac{1}{2} \left|( \sqrt{-x}- \sqrt{-y} )^2 ight| + \frac{1}{2}\left| ( \sqrt{-x}+ \sqrt{-y} )^2ight| =

    \frac{1}{2} ( \sqrt{-x}- \sqrt{-y} )^2 + \frac{1}{2}( \sqrt{-x}+ \sqrt{-y} )^2 =

    \frac{1}{2} (-x-2 \sqrt{xy}-y ) + \frac{1}{2}( -x+2\sqrt{xy}- y )=-x-y

    --------------------------

    \left|\frac{x+y}{2}-\sqrt{xy}}ight| +\left|\frac{x+y}{2}+\sqrt{xy}} ight| =|x|+|y|

    для любых действительных x и y, имеющих одинаковые знаки

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years