-
Решите, пожалуйста, очень надо.Задание на фотографии.
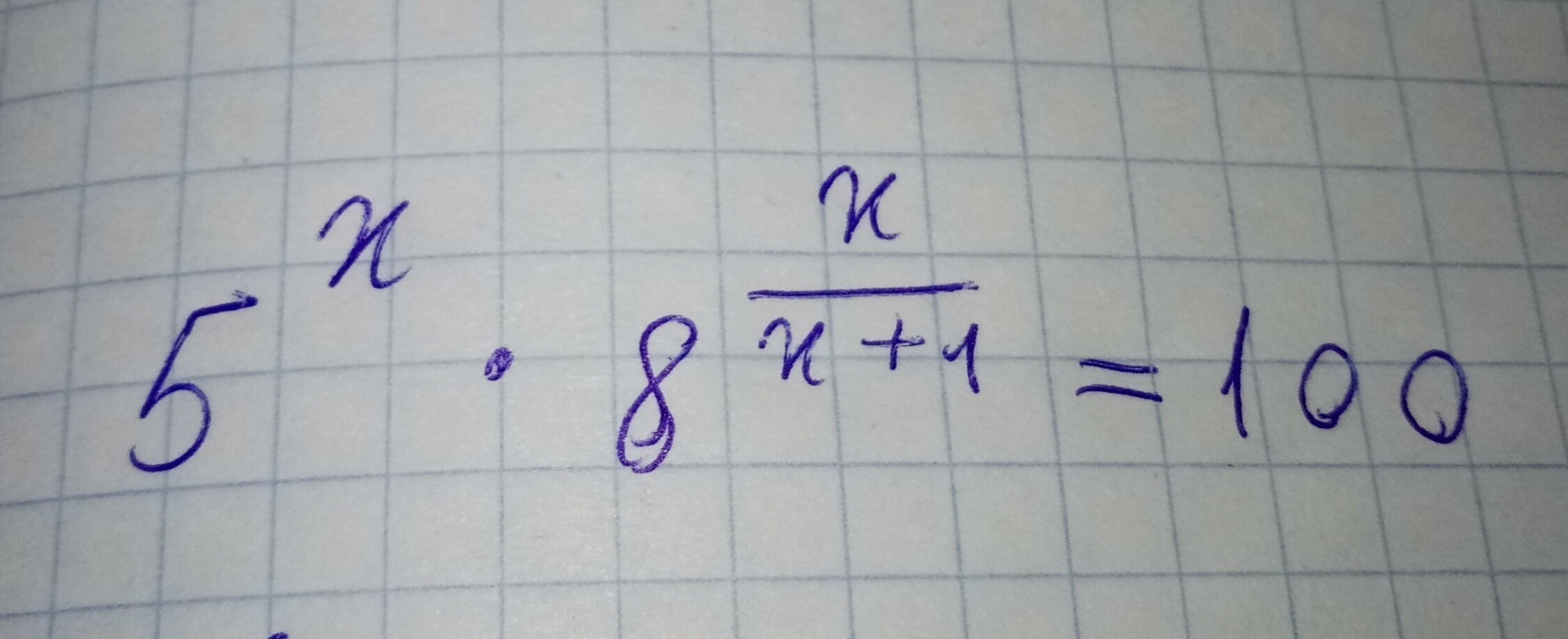
-
Предмет:
Алгебра -
Автор:
benjamínfkgv - 6 лет назад
-
Ответы 5
-
А можно это без логарифмов решить?
-
Автор:
jerimiah - 6 лет назад
-
0
-
-
Если честно, у меня других идей нет. Можно, конечно, было изначально заметить, что слева 5 * 2 и справа 5 * 2, составить систему x = 2 // 3x/(x+1) = 2 и получить корень 2, но тогда мы бы потеряли второй корень, поскольку сделали неравносильный переход.
-
Автор:
madisenhe1o - 6 лет назад
-
0
-
-
Ясно
-
Автор:
lanehurr - 6 лет назад
-
0
-
-
Ладно, спасибо большое
-
Автор:
kaitlin30 - 6 лет назад
-
0
-
-
1.
2.
Ответ:
-
Автор:
isaiasowen - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
4) задача: катер прошел расстояние между пристанями по течению реки за 2 часа, а обратный путь за 2,5 часа. Собственная скорость катера равна х км./ч, а скорость течения реки У км./ч.
Составьте выражение по условию задачи для нахождения: 1)Скорости катера по течению и против течения реки? 2)Расстояния, пройденного катером по течению реки? 3)Расстояния, пройденного против течения реки? 4) Общего расстояния, пройденного катером по течению реки и против течения реки? 5)Используя выражение из пункта(4), найдите его значение при у=2км/ч и х=18км/ч.
-
Предмет:
Математика -
Автор:
layla68 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Хочу стать полицейским кавалеристом
После какого класса уходить ? ( Сейчас в 9 )
Где учится ?
Как учатся ?
А если почти не занималась, научат ездить ?( Конным занималась 2 месяца, научилась ездить рысью. Потом переехали в другой город и возможности продалжать дальше заниматься нет. Сейчас почти год как занимаюсь ушу )
А где учат в Праге ?
Какие надо документы, если поступать в Прагу ?
Разкажите всё подробно
P.s. Отговаривать, шутить и т. п. и т. д. не надо!!!
Только по делу !-
Предмет:
Другие предметы -
Автор:
laylascwv - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Зделайте прошу План текста ноч перд рождиством прошу очень нужно
-
Предмет:
Литература -
Автор:
adánzudw - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожайлуста 3x+5x+y
How much to ban the user?
1 hour
1 day
100 years
