Задать вопрос Регистрация
Помочь другим

  • 100 баллов! Не пишите, пожалуйста, фигню, скрины из photomath и тому подобное. Мне нужно решение.

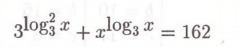
    question img

Ответы 2

  • Огромнейшее спасибо!!!!!!!

  • Замена: t=log_3x

    Надо ещё заменить x, выразим его по определению логарифма:

    log_3x=t\\x=3^t\\

    Итак, после замены, получаем следующее:

    3^{log^2_3x}+x^{log_3x}=162\\ \\ 3^{t^2}+(3^t)^t=162\\ \\ 3^{t^2}+3^{t^2}=162\\ \\ 2\cdot3^{t^2}=162\\ \\ 3^{t^2}=81\\ 3^{t^2}=3^4\\ t^2=4\\ t=б2

    Обратная замена:

    x=3^t\\ x=3^{б2}\\ \\ x_1=3^2=9\\ x_2=3^{-2}=\frac{1}{9}

    Учёт ОДЗ: x>0

    Оба корня подходят.

    Ответ: 1/9 и 9

    • Автор:

      brayan
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years