-
Помогите пожалуйста не могу решить задачу
На русском будет так, если |a|≠|b|≠|c| и a/(b+c) + b/(c+a)+c/(a+b)=1 то найти значение выражения (a^2/(b+c)+b^2/(c+a)+c^2/(a+b))÷(a+b+c)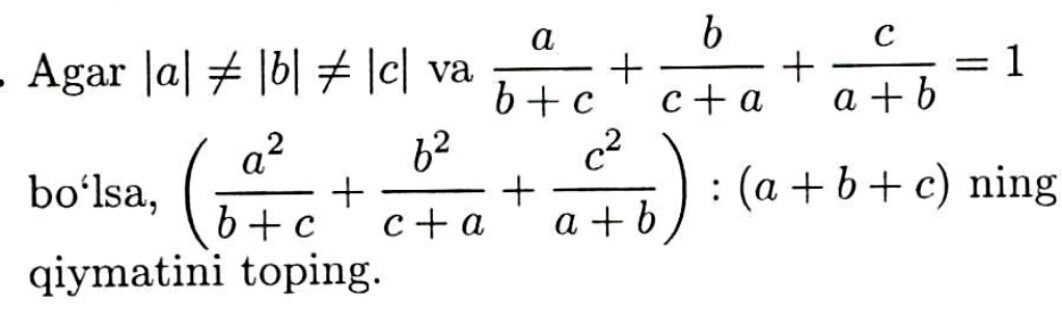
Ответы 3
-
Спасибо, объясни подробнее ты умножал первое равенство на a+b+c, потом ты из первое равенство получил (Вот это выражение не понял, как ты это получил) a^2/(b+c) + a + b^2/(c+a) + c^2/(a+b) +c =a+b+c. Подробнее пожалуйста, я должен объяснить учителю как это вышло?
-
Автор:
mini skirt51d7 - 6 лет назад
-
0
-
-
Всё дошло огромное спасибо, эту задачу не мог решить 2 дня
-
Автор:
maddox - 6 лет назад
-
0
-
-
Пусть a+b+c≠0, на него умножаем первое равенство
a(a+b+c)/(b+c) + b(a+b+c)/(c+a) + c(a+b+c)/(a+b) = a+b+c
a^2/(b+c) + a + b^2/(c+a) + b + c^2/(a+b) +c = a+b+c
a+b+c слева и справа сокращаются, остается
a^2/(b+c) + b^2/(c+a) + c^2/(a+b) = 0
т.к. a+b+c≠0, то
( a^2/(b+c) + b^2/(c+a) + c^2/(a+b) ) / (a+b+c) = 0
-
Автор:
britneystafford - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Просклоняйте порядковые числительные 1,5,9,10,31,21,125
-
Предмет:
Русский язык -
Автор:
kerrydecker - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Сколько детенышей рожает тигр?
-
Предмет:
Окружающий мир -
Автор:
verónicatate - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите плиз
ОЧЕНЬ СРОЧНООООООО
1.Delicious fruit ice cream (sell) there this week only.
2.Some interesting work (offer) to her before she moved to Spain.
3.Jim (speak) about when suddenly he entered the room.
4.Strict discipline will (insist) on.-
Предмет:
Английский язык -
Автор:
sailormcpherson - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
решите пож. 14,8:0,2 и объясн.
-
Предмет:
Математика -
Автор:
alexzanderrf7w - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
