-
решите пожалуйста очень срочно нужно желательно на листочке и подробно
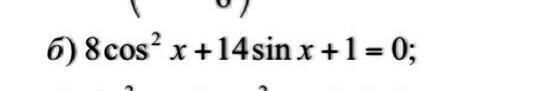
Ответы 2
-
8cos²x + 14sinx + 1 = 0
sin²x + cos²x = 1 ⇒ cos²x = 1 - sin²x
8( 1 - sin²x ) + 14sinx + 1 = 08 - 8sin²x + 14sinx + 1 = 0- 8sin²x + 14sinx + 9 = 08sin²x - 14sinx - 9 = 0Пусть sinx = a , a ∈ [ - 1 ; 1 ] , тогда8a² - 14a - 9 = 0D = (-14)² - 4•8•(-9) = 196 + 288 = 484 = 22²a₁ = (14 - 22)/16 = - 8/16 = - 1/2 ⇔ sinx = - 1/2 [ x = (-π/6) + 2πn[ x = (-5π/6) + 2πn , n ∈ Za₂ = (14 + 22)/16 = 36/16 = 9/4 = 2,25 ∉ [ - 1 ; 1 ]ОТВЕТ: (-π/6) + 2πn ; (-5π/6) + 2πn , n ∈ Z-
Автор:
louchase - 6 лет назад
-
0
-
-
8Cos²x + 14Sinx + 1 = 0
8(1 - Sin²x) + 14Sinx + 1 = 0
8 - 8Sin²x + 14Sinx + 1 = 0
8Sin²x - 14Sinx - 9 = 0
Sinx = m , - 1 ≤ m ≤ 1
8m² - 14m - 9 = 0
D = (- 14)² - 4 * 8 * (- 9) = 196 + 288 = 484 = 22²
m₂ = 2,25 - не подходит, так как 2,25 > 1
-
Автор:
julianneshannon - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Перевести предложение в Conditional Sentences
If l (to live) in 1703, I wouldn't have had a computer-
Предмет:
Английский язык -
Автор:
leylavise - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
6+x=11
Найди сумму неизвестного слагаемого-
Предмет:
Математика -
Автор:
graham - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Длина прямоугольного участка земли а м,а ширина на 80 м меньше.составь выражение для вычисления периметра участка.Вычисл , если : 1)а=260;2)а=500
-
Предмет:
Математика -
Автор:
jimmuyolsen - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Think! in three minutes write two reasons why you want to visit this national park.Use the phrases in Ex.4a.Tell your partner.
Нужно 4.б , помогите срочно !!!!!!
-
Предмет:
Английский язык -
Автор:
grey - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
