-
Помогите пожалуйста решить логарифмические выражения (15 б)
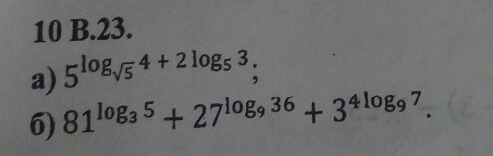
-
Предмет:
Алгебра -
Автор:
skylar3dvv - 6 лет назад
-
Ответы 7
-
ща допишу, времени не хватает
-
Автор:
diamond90 - 6 лет назад
-
0
-
-
готово
-
Автор:
leozbne - 6 лет назад
-
0
-
-
А где первое задание ?
-
Автор:
elf - 6 лет назад
-
0
-
-
ляяя
-
Автор:
beatriz - 6 лет назад
-
0
-
-
обнови
-
Автор:
ronniehensley - 6 лет назад
-
0
-
-
-
Автор:
tavianij3j - 6 лет назад
-
0
-
-
а)
Ответ: 144
б)
Ответ: 890
-
Автор:
angelo707 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Яка частина мови Рятуйте
-
Предмет:
Українська мова -
Автор:
nicholas4u6h - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ABCD - четырёхугольник, в котором диагонали AC и BD перпендикулярны и равны. Точка M не лежит в плоскости четырехугольника, а прямая MA перпендикулярна этой плоскости. Известно, что MA=MC=MD. Найдите углы четырёхугольника ABCD
Углы то я узнала чему равны, но мне нужно само решение
75, 75, 150, 60-
Предмет:
Геометрия -
Автор:
mollie59pf - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
пожалуйста помогите упражнения 5 дам 10 бал СРОООООООЧНААА
-
Предмет:
Английский язык -
Автор:
wyatt150 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Провідміняти слово кури, пожалуйста очень срочно!
-
Предмет:
Українська мова -
Автор:
genesis - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
