Задать вопрос Регистрация
Помочь другим

  • помогите,пожалуйста, очень срочно... буду очень благодарна

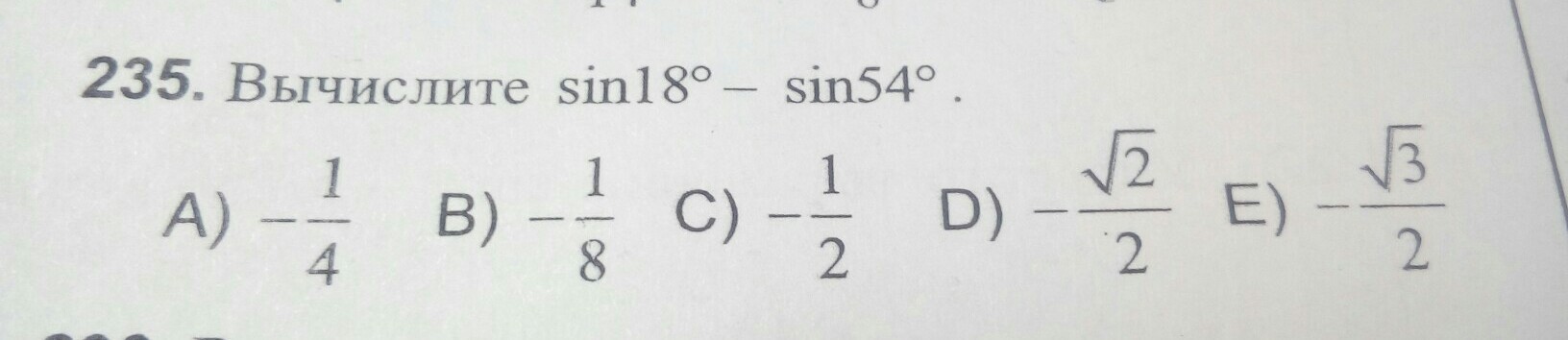
    question img

Ответы 2

  • огромное Вам спасибо!!❤❤❤

  • Рассмотрим сначала sin36° .

    sin36^\circ =sin(90^\circ -54^\circ )=cos54^\circ =cos(18^\circ +36^\circ )\; ,\\\\2sin18^\circ \cdot cos18^\circ =cos18^\circ \cdot cos36^\circ -sin18^\circ \cdot sin36^\circ \; ,\\\\2sin18^\circ \cdot cos18^\circ =cos18^\circ \cdot (\underbrace {1-2sin^218^\circ }_{cos36^\circ })-sin18^\circ \cdot \underbrace {2sin18^\circ \cdot cos18^\circ }_{sin36^\circ }\; ,\\\\2sin18^\circ =1-2sin^218^\circ -2sin^218^\circ \; ,\\\\4sin^218^\circ +2sin18^\circ -1=0\; ,\\\\t=sin18^\circ >0\; ,\; \; 4t^2+2t-1=0\; ,\; \; D=20\; ,

    t_{1,2}=\frac{-2\pm \sqrt{20}}{8}=\frac{-2\pm 2\sqrt5}{8}=\frac{-1\pm \sqrt5}{4}\; ,\\\\t_1=\frac{-1-\sqrt5}{4}<0\; \; ,\; \; t_2=\frac{-1+\sqrt5}{4}>0\; \; \Rightarrow \; \; sin18^\circ =\frac{\sqrt5-1}{4}\; .

    sin54^\circ =sin(90^\circ -36^\circ )=cos36^\circ =1-2sin^218^\circ =\\\\=1-2\cdot (\frac{\sqrt5-1}{4})^2=1-2\cdot \frac{6-2\sqrt5}{16}=1-\frac{6-2\sqrt5}{8}=\frac{8-6+2\sqrt5}{8}=\\\\=\frac{2+2\sqrt5}{8}=\frac{\sqrt5+1}{4}\; ;\\\\\\sin18^\circ -sin54^\circ =\frac{\sqrt5-1}{4}-\frac{\sqrt5+1}{4}=\frac{\sqrt5-1-\sqrt5-1}{4}=-\frac{2}{4}=-\frac{1}{2}

    • Автор:

      tommycain
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years