Задать вопрос Регистрация
Помочь другим

  • Укажите все целые решения дробно рационального уравнения.

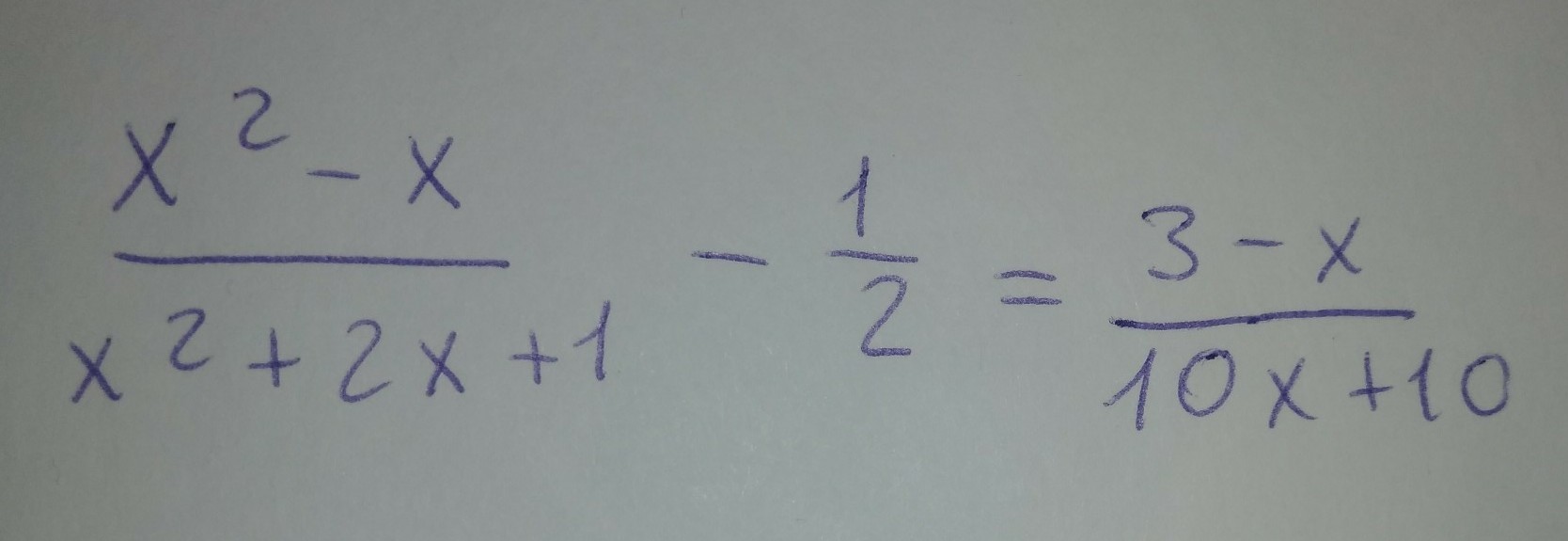
    question img

Ответы 1

  • \frac{x^2-x}{x^2+2x+1}-\frac{1}{2}=\frac{3-x}{10x+10}

    \frac{x^2-x}{(x+1)^2}-\frac{1}{2}=\frac{3-x}{10(x+1)}

    \frac{x^2-x}{(x+1)^2}-\frac{1}{2}-\frac{3-x}{10(x+1)}=0

    \frac{10*(x^2-x)-1*5*(x^2+2x+1)-(3-x)(x+1)}{10(x+1)^2}=0

    ОДЗ: x≠ -1

    10*(x^2-x)-1*5*(x^2+2x+1)-(3-x)(x+1)=0

    10x^2-10x-5x^2-10x-5-3x+x^2-3+x=0

    6x^2-22x-8=0

    Разделим обе части уравнения на 2 и получим:

    3x^2-11x-4=0

    D=121-4*3*(-4)=121+48=169=13^2

    x_1=\frac{11-13}{2*3}=\frac{-2}{6}=-\frac{1}{3}

    x_2=\frac{11+13}{2*3}=\frac{24}{6}=4

    Оба корня удовлетворяют ОДЗ, они не равны -1, но по условию решение должно быть целым, поэтому ответ: х = 4.

    • Автор:

      gloria52
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years