-
Решите пожалуйста с использованием метода неопределённых коэффициентов
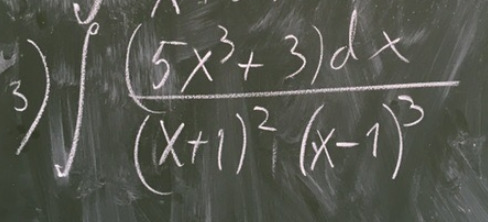
-
Предмет:
Алгебра -
Автор:
seamuse4da - 6 лет назад
-
Ответы 4
-
https://znanija.com/task/31677298
-
Автор:
fletcher40 - 6 лет назад
-
0
-
-
http://prntscr.com/mo6opo
-
Автор:
markussmall - 6 лет назад
-
0
-
-
Неверно:Решение системы:A1 = - 6; A2 = 37/4; A3 = 6; A4 = 31/4; A5 = 8.
-
Автор:
harpertbkn - 6 лет назад
-
0
-
-
A1/(x+1) + A2/(x+1)^2 + A3/(x-1) + A4/(x-1)^2 + A5/(x-1)^3
Приводим к общему знаменателю (x+1)^2(x-1)^3. Числитель такой будет:
A1(x+1)(x-1)^3 + A2(x-1)^3 + A3(x+1)^2(x-1)^2 + A4(x+1)^2(x-1) + A5(x+1)^2 =
= A1(x^4-2x^3+2x-1) + A2(x^3-3x^2+3x-1) + A3(x^4-2x^2+1) +
+ A4(x^3+x^2-x-1) + A5(x^2+2x+1) =
= x^4(A1+A3) + x^3(-2A1+A2+A4) + x^2(-3A2-2A3+A4+A5) + x(2A1+3A2-A4+2A5) + (-A1-A2+A3-A4+A5) = 5x^3+3
Коэф-ты при одинаковых степенях должны быть равны. Система:
{ A1+A3 = 0; x^4
{ - 2A1+A2+A4 = 5; x^3
{ - 3A2-2A3+A4+A5 = 0; x^2
{ 2A1+3A2-A4+2A5 = 0; x
{ - A1-A2+A3-A4+A5 = 3; 1
Я не буду расписывать эту систему, она достаточно простая. Решение системы:
A1 = - 3/2; A2 = 1/4; A3 = 3/2; A4 = 7/4; A5 = 2.
Подставляем в интеграл:
S (-3/2)/(x+1) dx + S (1/4)/(x+1)^2 dx + S (3/2)/(x-1) dx + S (7/4)/(x-1)^2 dx + S 2/(x-1)^3 dx =
= - 3/2*Ln |x+1| - 1/(4(x+1)) + 3/2*Ln |x-1| - 7/(4(x-1)) - 1/(x-1)^2 + C
Я специально написал логарифмы с большой буквы Ln, чтобы не путать букву l со знаком модуля |.
-
Автор:
derrickezki - 6 лет назад
-
0
-
-
Добавить свой ответ
- Можно ли утверждать что правление Данила Галицкого было периодом расцвета галицко-волынского княжества. свой ответ обоснуйте
-
пожалуйста,ПОМОГИТЕ,заданием 16 т3 ц*4-(28т-25т 87кг)*6=?плиз плиз плиз
-
Предмет:
Математика -
Автор:
rebeccayehf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
решите пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста помогите мне пожалуйста
-
Предмет:
Математика -
Автор:
bransonhnhi - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Установление просоветских режимов в ГДР
-
Предмет:
История -
Автор:
embermckinney - 6 лет назад
-
Ответов:
1 -
Смотреть
-
