-
Никак не могу разобраться с решением! Второе ещё осилила, хотя не до конца, а вот первое не получается, помогите плиз! Решите первое
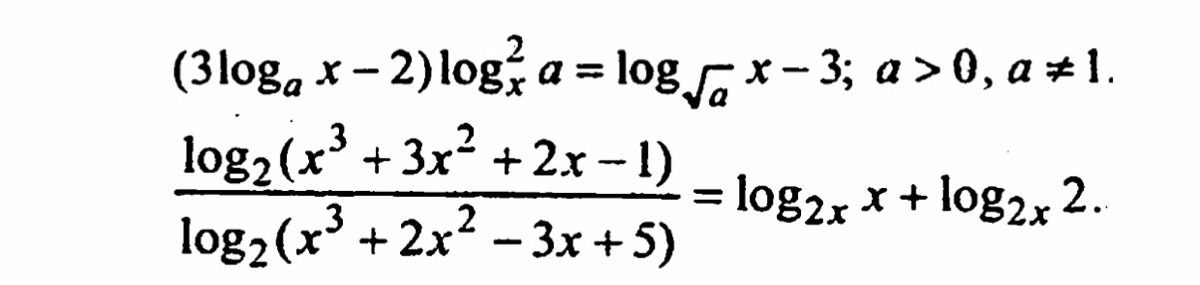
-
Предмет:
Алгебра -
Автор:
cheyennei7kw - 6 лет назад
-
Ответы 1
-
x>0
x≠1
Замена переменной
{3t-2-2t³+3t²=0
{t≠0
3t+3t²-2(1+t³)=0
3t(1+t)-2(1+t)(1-t+t²)=0
(1+t)(3t-2+2t-2t²)=0
t=-1 или -2t²+5t-2=0
-2t²+5t-2=0
2t²-5t+2=0
D=9
t=
или t=2
Обратный переход
logₐx=-1 ⇒ x=a⁻¹⇒x=
logₐx=
⇒ x=√a
logₐx=2 ⇒ x=a²;
-
Автор:
airesraug - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Знайдіть площу паралелограма, діагоналі якого утворюють ку 30° та дорівнюють 3 см і 6 см
-
Infinitive and Gerund 1. Put “to” before the infinitive where it is necessary.
1 . My son asked me__let him __ go to the club.
2 . You must make him__practice an hour a day.
3 . She was made__repeat the song.
4 . e is not sure that it can__be done, but he is willing__ try.
5 . Let me__help you with your work.
6 . She asked me__read the letter carefully and__ write an answer.
7 . You ought__take care of your health.
8 . 1 looked for the book everywhere but could not__find it.
9 . He was seen __leave the house.
10 . We had __put on our overcoats because it was cold.
-
Предмет:
Английский язык -
Автор:
ozziemorse - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
35б! Задание на фото. Нужно написать про Walt Disney
-
Предмет:
Английский язык -
Автор:
dingo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
sin79 sin49 + cos79 cos49
-
Предмет:
Математика -
Автор:
carmelo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
