-
Решите уравнение 1+x+x^2+...x^99=0. Заранее благодарю
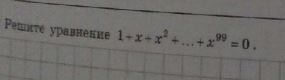
-
Предмет:
Алгебра -
Автор:
cheyanneowen - 6 лет назад
-
Ответы 1
-
1+x+x^2+..+x^99 =
= 1+x+x^2+x^3+x^4+x^5...+x^98+x^99 =
= 1+x+x^2(1+x)+x^4(1+x)...+x^98(1+x) =
= (1+x)(1+x^2+x^4+...+x^98) = 0
Данное уравнение равносильно двум уравнениям:
1+x=0, откуда х = -1
1+x^2+x^4+...+x^98 = 0 - решений нет, так как все степени чётные
Исходное уравнение имеет только один корень: х = -1
-
Автор:
kyanfritz - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
составьте рассказ от имени путешественника посетившего древние пирей и Афины Включите в рассказ описание морских гаваней длинных стен керамика агоры акрополя
-
Предмет:
История -
Автор:
elisechapman - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите пожалуйсто ,спишыце, устауляючы прапушчаныя спалучэнни литар.растлумачце их написанне
-
Предмет:
Беларуская мова -
Автор:
thornton - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
итоги борьбы за независимость в странах Латинской Америки
ОЧЕНЬ СРОЧНО1!1!!!!! -
За 1 час ПО ПРОСЕЛОЧНОЙ ДОРОГЕ автобус проезжает 30 километров. Автобус находился в пути 7/3 часа. Сколько километров он проехал?
-
Предмет:
Математика -
Автор:
nathalieabbott - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
