-
помогите, пожалуйста, необходимо найти площадь криволинейной трапеции (с графиками)
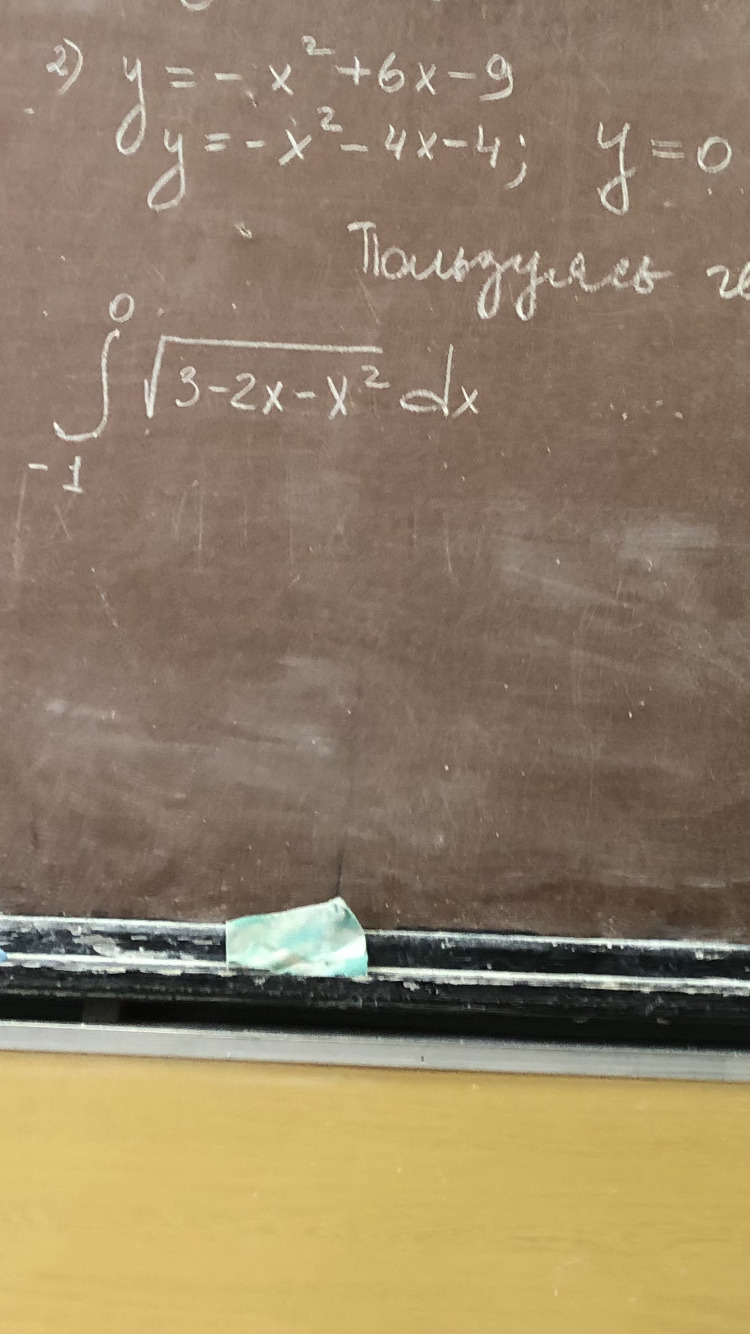
-
Предмет:
Алгебра -
Автор:
giggles30st - 6 лет назад
-
Ответы 1
-
Даны уравнения парабол: у = -х² + 6х - 9 и у = -х² - 4х - 4.
Если их преобразовать, выделив полные квадраты, то получим:
у = -(х - 3)² и у = -(х + 2)².
Точки х = -2 и х = 3 при у = 0 это координаты вершин парабол.
Найдём точку пересечения парабол:
-х² + 6х - 9 = -х² - 4х - 4.
10х = 5,
х = 5/10 = 1/2.
Отсюда искомая площадь разбивается на 2 участка: (-2; (1/2)) и ((1/2); 3).
Площадь равна сумме интегралов:

-
Автор:
calderon - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Какое прилагательное не имеет простой формы сравнительной степени?
Выберите вариант ответа:
Голый
Босой
Сладкий
Гладкий
Горький-
Предмет:
Русский язык -
Автор:
mittensuile - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
В одной из клеток доски 5×5
5
×
5
(5 строк, 5 столбцов) стоит фишка. За один ход можно передвинуть её на соседнюю по углу клетку, либо на одну клетку вправо, либо на одну клетку влево. Какое наибольшее количество ходов можно сделать так, чтобы фишка не побывала ни в какой клетке дважды?Буду ОООЧЕНЬ благодарен!!-
Предмет:
Математика -
Автор:
bruiserewll - 6 лет назад
-
Ответов:
3 -
Смотреть
-
- Рассчитайте относительную плотность брома по кислороду
-
Какое утверждение неверно по отношению к этому высказыванию?
Каждый охотник желает знать, где сидит филин.
Выберите вариант ответа:
есть только одно слово, в котором все согласные звуки твёрдые.
звук [й'] встречается два раза.
есть только одно слово, в котором количество букв меньше, чем количество звуков.
есть только одно слово, в котором количество букв больше, чем количество звуков.
звук [о] встречается только один раз.-
Предмет:
Русский язык -
Автор:
twinkle - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
