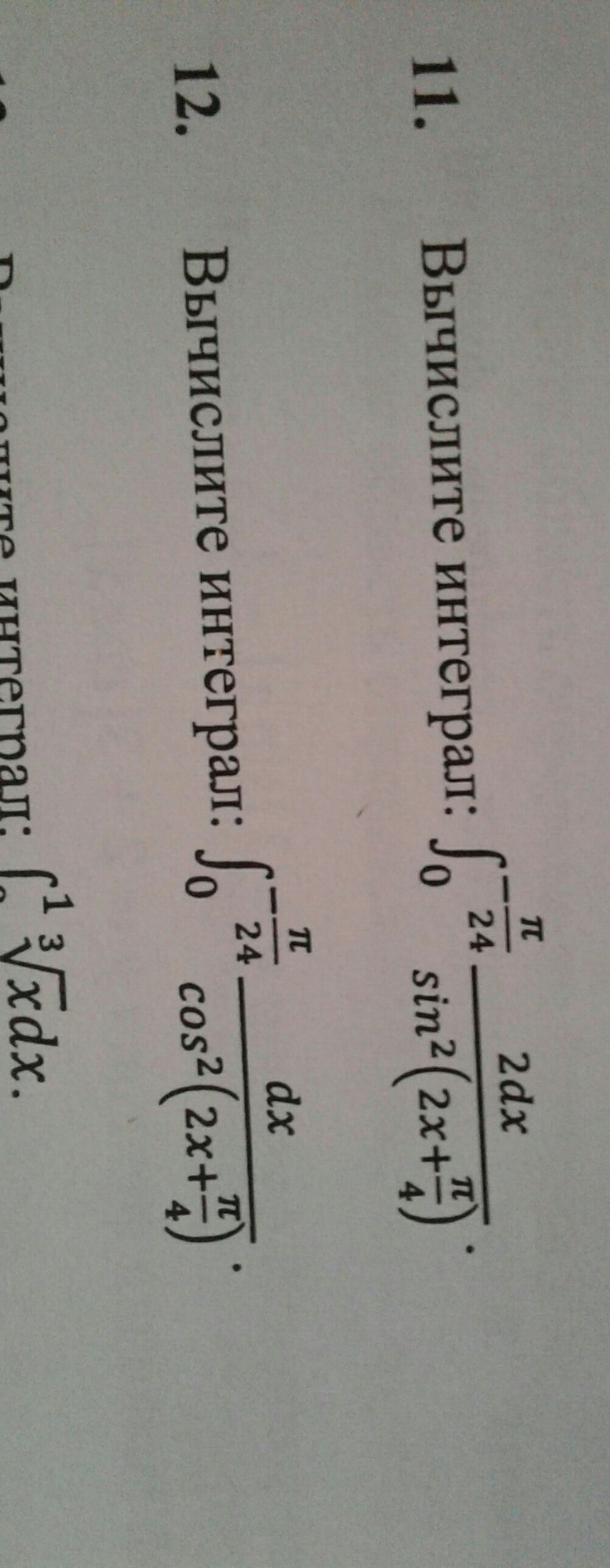Ответы 1
-
11.
Нашёл неопределённый интеграл и подставил значения -pi/24 и 0, при чём так что если получившиеся функция это F, то F(-pi/24)-F(0), это и есть определённый интеграл
12.
-
Автор:
coralieve2m - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
представьте в виде многочлена
1)(3y+2)²
2)(a²+3)(3-a²)
3)-x(2x+5)
4)(2a-9b)(2a+9b)
5)-3c²(2c-1)
6)(a-1)(a+3)
7)(-7k+1)²-
Предмет:
Алгебра -
Автор:
nathanlopez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите срочно! пожалуйста прошууууууууууууууууууу
-
Предмет:
Математика -
Автор:
greta84 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста решить пример. Фото прикрепила ниже. Заранее спасибо!
*там опечатка - 12ab-
Предмет:
Алгебра -
Автор:
punkinbean - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В 2 часа дня от пристани отошёл прогулочный катер и поплыл вниз по течению. Через 4 часа вслед за ним вышла моторная лодка со скоростью 15 км/ч и через четыре часа обогнала катер. Найдите скорость катера, если скорость течения реки 2 км/ч?
А) 8 км/ч
Б) 6 км/ч
В) 12 км/ч-
Предмет:
Математика -
Автор:
tannertswh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years